planimeria Tomek: Oblicz sumę długości przekątnych rombu, gdy długość boku wynosi 2.5 a promień okręgu wpisanego w romb wynosi 1.2

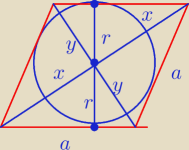
Janek191: P = a* h = a*2 r = 2,5 * 2,4 = 6

	3
P = 0,5 *2x*2y = 2x*y = 6 ⇒ x*y = 3 ⇒ y =
	x

oraz x² + y² = a²

	9
x2 +		= 6,25 / * x2
	x2

x⁴ − 6,25 x² + 9 = 0 / * 4 4 x⁴ − 25 x² + 36 = 0 Δ = 625 − 4*4*36 = 625 − 576 = 49 √Δ = 7

	25 + 7
x2 =		= 4 ⇒ x = 2
	8

	3
y =		= 1,5
	2

Odp. e = 2 x = 4 f = 2 y = 3 e + f = 7 =======

Tomek: no taak nie uwzględniłem twierdzenia pitagorasa i nie mogłem ruszyć dzięki wielkie

5-latek: jest jeszcze inny wzor na pole czworokata wpisqaneo w okrag P= √(p−a)(p−b)(p−c)(p−d) gdzie p to polowa obwodu i a,b, c d to dlugosc bokow