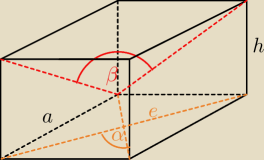
trygonometria Filippo: Przekątne podstawy prostopadłościanu mają długość 5, a cosinus kąta między nimi jest równy ⁷₂₅. Oblicz cosinus kąta między przekątnymi dwóch ścian bocznych wychodzącymi z jednego wierzchołka, jeżeli wysokość prostopadłościanu jest równa 2√3. Dane: e=5 cosα=⁷₂₅ h=2√3 cosβ=? Obliczenia: z tw. cosinusów a²=2,5²−2,5²−2*2,5*2,5*cosα a²=6,25+6,25−2*6,25*⁷₂₅ a²=12,5−3,5 a=√9 a=3 d²=h²+a² d²=(2√3)²+3² d²=12+9 d=√21 I jak dalej wyliczyć cos β? Dalej z twierdzenia cos? czy jakoś inaczej ? i czy moje obliczenia są dobre? Proszę o pomoc

Filippo: a²=2,5²+2,5²−2*2,5*2,5*cosα − mała poprawka w pierwszej linijce obliczeń zamiast plusa napisałem minus

Filippo: Dzięki za pomoc... dałem radę