zadanko Blue: Mógłby ktoś wytłumaczyć to zadaniebo nie ogarniam: Zbiór A ma tę własność, że poprzez usuwanie z niego jednego lub dwóch elementów można utworzyć 190 różnych zbiorów. Ile elementów ma zbiór A ?

Janek191: Może tak :

n n −1		n n − 2
	+		= 190

Mila: 19 ?

YushokU: Dołączam się do prośby To jest rozwiązanie, ale trochę go nie rozumiem. http://oi59.tinypic.com/1zzsug1.jpg @Blue Jak poszła maturka?

Mila: Jeżeli usuwasz 1 element ze zbioru A to zostają pozostałe elementy i to jest nowy zbiór,

	n 1
Jeden element można wybrac ze zbioru n− elementowego na		sposobów.

Jeżeli usuwasz dwa elementy ze zbioru A to zostają pozostałe elementy i to jest nowy zbiór.

	n 2
Dwa elementy można wybrać na		sposoby.

Ponieważ w treści jest spójnik "lub" to łączymy ilości tych zbiorów:

n 1		n 2
	+		=190

	1
n+		*n*(n−1)=190
	2

2n+n*(n−1)=380 n(2+n−1)=380 n*(n+1)=380 w zbiorze N₊ mamy iloczyn kolejnych liczb naturalnych, zatem zgaduję : 19*20=380 n=19 === po usunięciu jednego elementu ( na wszystkie sposoby) otrzymamy 19 zbiorów o 18 elementach po usunięciu 2elementów ( na wszystkie sposoby)otrzymamy

19 2		1
	=		*19*18=19*9=171 różnych podzbiorów o 16 elementach
		2

171+19=190.

Jacek: Niestety, moim zdaniem, zadanie ma nieprecyzyjną treść. Bo chodzi o jednokrotne usunięcie jednego lub dwóch elementów ze zbioru i 190 oznacza liczbę różnych zbiorów powstałych z takiego jednokrotnego aczkolwiek alternatywnego działania. W powyższym rozwiązaniu przyjęto trochę inne rozumowanie, ale na jedno wychodzące, czyli na ile sposobów można wybrać różne zbiory o 1 mniej liczne od n ze zbioru n−elementowego, no i podobnie z n−2. Osobiście napisałbym:

n 1		n−1 n−1		n 2		n−2 n−2
	*		+		*

, ale na to samo wychodzi.

YushokU: Ahaaaaa. Dziękuję Milu . Totalnie źle zrozumiałem polecenie. Myślałem, że chodzi o to, że przypuścmy mamy zbiór {A,B,C,D} i usuwając z niego 1 element (np.D) możemy mieć z niego zbiory {A},{B},{C},{A,B},{A,C},{B,C},{A,B,C} No i nie miałem pojęcia jak się za to zabrać. Ale teraz po twoim rozwiązaniu dokładnie rozumiem treść polecenia i widzę swój błąd rozumowania

Mila:

Blue: Nadal średnio to ogarniam..

Blue: Ogólnie matura dobrze poszła, z wyjątkiem tego zadania i tego trapezu, z tym że rozwiązanie trapezu rozumiem, a tego nie...

Blue: otrzymamy 19 zbiorów o 18 elementach 171 różnych podzbiorów o 16 elementach skąd się to wzięło?

Blue: ej, już chyba ogarniam, ale czy tam nie powinno być 171 różnych podzbiorów o 17 elementach

Jacek: tak, masz rację, 171 razy 17 elementowe zbiory

Janek191: n = 19 − mamy zbiór o 19 elementach Wybieramy z niego podzbiory 18 − elementowe i 17 − elementowe. Jest ich

19 18		19 17		19 !		18*19
	+		= 19 +		= 19 +		=
				2 * 17 !		2

= 19 + 9*19 = 19 + 171 = 190

Mila: Zrób symulację na zbiorze Z={A,B,C,D} Wyjmujesz jeden element: A zostają {B,C,D} albo B zostają {A,C,D} albo C zostają {A,B,D} albo D zostają {A,B,C} Masz 4 nowe zbiory , każdy ma 3 elementy ze zbioru Z.

Blue: To dobrze W każdym razie dzięki wielkie Mila za wytłumaczenie Ale zadanko bardzo nietypowe jak na maturę.

Mila: No źle odjęłam 19−2=17.

Mila: Tak , a z trapezem jakie było?

Blue: Chodzi mi o 17 http://www.cda.pl/video/9517328/Atak-na-Wall-Street-online-2013-Napisy-PL-HD

Blue: http://www.zadania.info/d1631/82527 hahah, nie ten link skopiowałam

kyrtap: jeszcze nie śpicie Królewny ?

Blue: Ja jak zwykle się nie wyśpię A Ty królewiczu?

Blue: Na Googlach jest jakaś matematyczka dziś, tak nawiasem mówiąc

kyrtap: za wczesna pora dla studenta

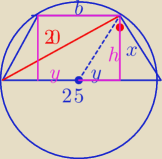
Janek191: x² = 25² − 20² = 625 − 400 = 225 x = 15 Pole P_Δ = 0,5*20*15 = 150 P_Δ = 0,5*25*h = 12,5 h = 150 ⇒ h = 12 y² = r² − h² = 12,5² − 12² = 156,25 − 144= 12,25 y = 3,5 b = 2 y = 5 Pole trapezu P = 0,5 *( 25 + 5)*12 = 15*12 = 180 ===========================

YushokU: No to Blue widzę, że podobne problemy mamy Swoją drogą to maturki z zadania.info z tygodnia na tydzień są co raz fajniejsze.

YushokU: @Janek191 Zrobiłeś 14, a nie 17'ste I odpowiedź nieco inna niż prawidłowa(192)

Blue: Janek, to zadanie akurat umiałam Chodziło o inny trapez i wyszło 192, a nie 180

Qulka: a to po prostu były trójkąty 3x:4x:5x i po co się męczyć z pitagorasem b=7

Blue: Dobrze, że zadania.info robią te maturki, można się sprawdzić Bo jednak materiałów do nowej matury nie ma aż tak dużo

Blue: Ja jak to liczyłam, to wykorzystałam trójkąt prostokątny i potem z pola trójkąta h i z Pitagorasa znowu

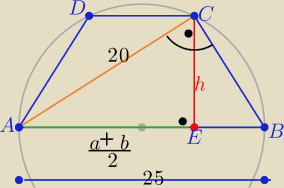
Eta: |BC|= √625−400=15

	20*15		a+b
h=		= 12 i |AE|=		=√400−144=16
	25		2

P=16*12=192

Qulka: 99% zadań z trójkątem prostokątnym to ten 3:4:5 można się nie męczyć

Janek191: Bo pomyłka − powinno być b = 2*3,5 = 7 P = 0,5*( 25 + 7)*12 = 6*32 = 192 ========================

Eta: Żadna "męka"