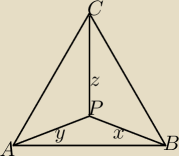
Trójkąt równoboczny - dowód z twierdzenia cosinusów Kamil: Trójkąt ABC jest trójkątem równobocznym. Udowodnij, że jeśli kąt APB ma 150 stopni to: z² = y² + x² Rozumiem, że muszę skorzystać z twierdzenia cosinusów, otrzymuję równania: a²=x²+y² − 2xycos150 = x² + y² + √3xy a² = y² + z² − 2yzcosβ a² = x² + z² − 2xycosγ oraz β+γ = 210 stopni Może jakaś mała podpowiedź, co trzeba zrobić dalej? Bo nie dostrzegam drogi do rozwiązania.

Janek191: (360^o − 150^o ) : 2 = 105%{o} więc β = γ = 105^o

Janek191: Pewnie mnie rysunek zmylił. Nie musi być symetryczny .

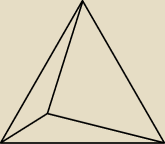
Kamil: Prawda tylko w jedynym, szczególnym przypadku, jednak możemy skonstruować punkt P w innym i wtedy np. β = 130 γ = 80. Potrzebuję bardziej ogólnego rozwiązania.