Planimetria Mateusz: Długości przekątnych równoległoboku są równe 8 i 12 cm a kąt między nimi ma miarę 60 stopni. Oblicz pole tego równoległoboku. Proszę o pomoc, próbowałem boki liczyć z tw. cosinusów ale nie wychodzi...

matik:

	1
masz dwa trójkąty o polu P=		*4*6*sin60
	2

	1
oraz dwa trójkąty o polu P=		*4*6*sin120
	2

Mateusz: Ok, thx. Teraz już pójdzie. Łatwa sprawa ale dziwne że z cosinusów zawsze oba boki równoległoboku wychodziły mi takie same

5-latek:

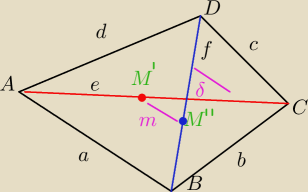
	1
jest tez gotowy wzor P=		e*f*sinδ gdzie δ to kat miedzy przekatnymi
	2

Masz tu ogolnie dla czworokata wypuklego: A,B C D są to katy czworokata a.b.c d. boki tego czworokata M' i M" to srodki przekatnych m= |M'M"| Mamy tak a²+b²+c²+d²= e²+f²+4m²

	1		1
Pczw=		a*b*sinB +		c*d*sinD
	2		2

W rownolegloboku a=c i b=d i m=0 e²+f²= 2(a²+b²) P= a*b*sinB Drugi wzor masz na gorze e²*f²= a²*c²+b²d²−2abcdcos2w gdzie 2w=A+C lub B+D Jesli czworokat jest wpisany w kolo to 2w=180^o e*f= a*c+b*d (Twierdzenie Ptolemeusza