optymalizacja ekstremum iii geometrykz: do sprawdzenia: "przekrój osiowy stożka jest trójkątem o obwodzie 24. Jakie wymiary musi mieć ten stożek, aby jego objętość była jak największa?" V− max 2l+2r=24 l+r=12 ⇒ l = 12−r tw. Pitagorasa: h²+r²=l² h=√144−24r, r∊(0,6)

	1
V(r)=		*π*r2*(√144−24r)
	3

	1
V(r)= √(144−12r)(		π2r4)
	9

V(r) największe, gdy pod pierwiastkiem wartość jest największa

	24		96
V'(r)=−		π2r4+64π2r3−		π2r3 z: [f(x)*g(x)]'
	9		9

	24		96
V'(r) = 0 ⇔ −		π2r4+64π2r3−		π2r3 = 0
	9		9

480		24
	π2r3=		π2r4
9		9

24r=480 r=20 co jest sprzecznością. co pokręciłem?

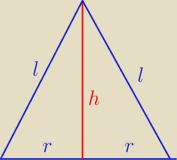
Janek191: Mamy 2 r + 2 l = 24 ⇒ r + l = 12 ⇒ l = 12 − r więc h² = l² − r² = ( 12 − r)² − r² = 144 − 24 r + r² − r² = 144 − 24 r h = √ 144 − 24 r r ∊ ( 0 , 6 ) =============

	1		1
V =		π r2 *h =		π r2 *√144 − 24 r
	3		3

	π
V (r) =		*√ 144 r4 − 24 r5
	3

	π
V '(r) =		*U{ 576 r3 − 120 r4}}{ 2 √ 144 r4 − 24 r5} = 0 ⇔ r = 4,8
	3

więc h = √ 144 − 24*4,8 = √ 144 − 115,2 = √28,8 = 2√7,2 l = 12 − 4,8 = 7,2

Janek191:

	π		576 r3 − 120 r4
V'( r) =		*
	3		2 √ 144 r4 − 24 r5

geometrykz: nie rozumiem co się stało w V'(r) coś jakby pochodna z tego co pod pierwiastkiem dzielona na dwukrotność tego pierwiastka, ale skąd to się bierze? pierwszy raz coś takiego widzę.

Janek191: Pochodna funkcji złozonej :

	1
(√g(x))' =		* (g(x)) '
	2√g(x)

geometrykz: a nauczycielka mowiła, że w liceum tego nie ma. dzięki.