funkcja homograficzna Dawid: Witam, czy ktoś mógłby łopatologicznie wytłumaczyć mi podpunkt b, nie wiem kompletnie co tu nalezy zrobić... a) Naszkicuj wykres funkcji F(x) = |−2+3x+1|, gdzie x ∈ R −{−1} b) Ustal, dla jakich wartości parametru m(m∈R), równanie F(x) = m+3m+2 ma dwa rozwiązania różnych znaków

J: trzeba tak dobrać m, aby prosta: 4m + 2 przecinała wykres a) w dwóch punktach

J: oczywiście w dwóch punktach o róznych znakach odciętych

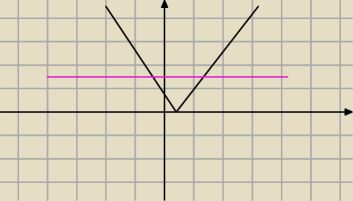
J: ustal dla jakiego m różowa prosta przecina wykres w dwóch punktach, których odcięte są róznych znaków

Dawid: przepraszam

Dawid:

	m+3
w b jest pomyłka bo F(x) =
	m+2

Dawid: w podreczniku wlasnie jest cos z funkcja stala ale przeciez funkcja z podpunktu b za chiny nie bedzie stala tylko homograficzna

J:

	m+3
dla ustalonego m , jest liczbą .... masz:		> 1
	m+2

Dawid:

Dawid: nierozumiem

J: Rozwiaz nierownosc

Dawid: no tak ale skad ona sie wzieła?

J: Bo rozowa prosta musi lezec nad punktem 1

Dawid: no ale to nie bedzie prosta tylko kolejna hiperbola..

Dawid:

	m+3
F(x) =		− to nie jest wzor na jakas prostą
	m+2

J: Dla konkretnego m to bedzie prosta y = k

Mila:

	m+3
Cały ułamek		traktujesz jako parametr ( dla konkretnego m będzie to liczba) i jego
	m+2

wartość ma być większa od F(0). Ta funkcja F(x)=|−2+3x+1| to mi jakoś niedobrze wygląda to jaki ma wzór F(x) ?

Dawid: F(x) = |−2+³_x+1| − sorki ze tutaj tez nie zrobilem ulamka

Dawid:

	3
F(x) = |−2+		|
	x+1

Dawid:

	m+3
jak jest że		>1 to wychodzi że m>−3 , musi byc jeszcze mniejsze od 2 i wtedy
	m+2

wuchodzi że m ∊ (−∞,−2)∪(−1,+∞) ale w odpowiedzi że m ∊(−1,+∞)

Dawid: co ja mam zrobić

Mila:

	3
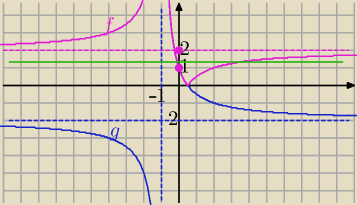
Rysujemy wykres F(x)=|−2+		|, x≠−1
	x+1

	m+3
y=
	m+2

m+3
	≥0 i m≠−2⇔m<−3 lub m>−2
m+2

	3
1) g(x)=−2+
	x+1

2) symetria względem OX , tej części wykresu co leży pod osią OX⇒

	3
F(x)=|−2+		|
	x+1

Zielona linia może przeciąć wykres F(x) w dwóch punktach takich, że x₁<0 i x₂>0 tylko gdy y∊(1,2)

	m+3
1<		<2 ⇔
	m+2

	m+3		m+3
1<		i		<2 po rozwiązaniu
	m+2		m+2

m>−2 i ( m<−2 lub m>−1)⇔m>−1⇔ m∊(−1,∞)

Dawid: dziękuję bardzo, juz wiem co zle robilem

Mila: