stereometria
SiA:
Bardzo proszę o pomoc w tym zadaniu .
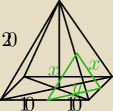
w ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakową długość równą 20.
Ostrosłup przecięto płaszczyzną przechodzącą przez środki krawędzi wychodzących z jednego
wierzchołka przy podstawie. Oblicz
a)pole otrzymanego przekroju
b)odległość tej płaszczyzny od punktu wspólnego tych krawędzi
Odpowiedź: a) 50, b) 5
√2
Przekrój jest trójkątem
z tw. o linii łączącej środki boków w trójkącie wyliczyłam że że boki x=10 ( bo będą one 2 razy
mniejsze od boku trójkąta równego 20.
Następnie bok przekroju y wyliczyłam z tw. Pitagorasa y
2=10
2+10
2⇒y=10
√2
A więc pole tego przekroju obliczyłam ze wzoru Herona i wyszło mi 50 tylko teraz kompletnie nie
wiem jak zrobić podpunkt b. Bardzo proszę o jakąkolwiek pomoc

22 mar 12:49
SiA: okey już nie trzeba sama zrobiłam
22 mar 13:09
SiA:
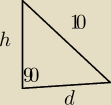
tylko nie wiem czy dobrze to wyliczyłam bo założyłam że ta odległość to d w narysowanym
trójkącie h to wysokość przekroju którą można wyliczyć z tw. Pitagorasa
wynosi ona 5
√2 a więc następnie korzystamy z Tw. Pitagorasa i d wychodzi nam że się róna
5
√2 ale kompletnie nie wiem czy dobrze wyznaczyłam tą odległlość
22 mar 13:22
 Bardzo proszę o pomoc w tym zadaniu .
w ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakową długość równą 20.
Ostrosłup przecięto płaszczyzną przechodzącą przez środki krawędzi wychodzących z jednego
wierzchołka przy podstawie. Oblicz
a)pole otrzymanego przekroju
b)odległość tej płaszczyzny od punktu wspólnego tych krawędzi
Odpowiedź: a) 50, b) 5√2
Przekrój jest trójkątem
z tw. o linii łączącej środki boków w trójkącie wyliczyłam że że boki x=10 ( bo będą one 2 razy
mniejsze od boku trójkąta równego 20.
Następnie bok przekroju y wyliczyłam z tw. Pitagorasa y2=102+102⇒y=10√2
A więc pole tego przekroju obliczyłam ze wzoru Herona i wyszło mi 50 tylko teraz kompletnie nie
wiem jak zrobić podpunkt b. Bardzo proszę o jakąkolwiek pomoc
Bardzo proszę o pomoc w tym zadaniu .
w ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakową długość równą 20.
Ostrosłup przecięto płaszczyzną przechodzącą przez środki krawędzi wychodzących z jednego
wierzchołka przy podstawie. Oblicz
a)pole otrzymanego przekroju
b)odległość tej płaszczyzny od punktu wspólnego tych krawędzi
Odpowiedź: a) 50, b) 5√2
Przekrój jest trójkątem
z tw. o linii łączącej środki boków w trójkącie wyliczyłam że że boki x=10 ( bo będą one 2 razy
mniejsze od boku trójkąta równego 20.
Następnie bok przekroju y wyliczyłam z tw. Pitagorasa y2=102+102⇒y=10√2
A więc pole tego przekroju obliczyłam ze wzoru Herona i wyszło mi 50 tylko teraz kompletnie nie
wiem jak zrobić podpunkt b. Bardzo proszę o jakąkolwiek pomoc 
 tylko nie wiem czy dobrze to wyliczyłam bo założyłam że ta odległość to d w narysowanym
trójkącie h to wysokość przekroju którą można wyliczyć z tw. Pitagorasa
wynosi ona 5√2 a więc następnie korzystamy z Tw. Pitagorasa i d wychodzi nam że się róna
5√2 ale kompletnie nie wiem czy dobrze wyznaczyłam tą odległlość
tylko nie wiem czy dobrze to wyliczyłam bo założyłam że ta odległość to d w narysowanym
trójkącie h to wysokość przekroju którą można wyliczyć z tw. Pitagorasa
wynosi ona 5√2 a więc następnie korzystamy z Tw. Pitagorasa i d wychodzi nam że się róna
5√2 ale kompletnie nie wiem czy dobrze wyznaczyłam tą odległlość