Proszę o pomoc nie mam już sił :/
Maciej: a) log4(log2(x+2))<1
b) log x+12x≥1
22 mar 11:59
Frost: w a) musisz mieć założenie
log
2(x+2)>0
log
2(x+2)> log
21 2>1więc
x+2>1
x>−1
log
4[log
2(x+2)]<1
log
4[log
2(x+2)]< log
44 4>1 więc
log
2(x+2)<4
log
2(x+2)<log
216 2> 1 zatem
x+2<16
x<14
odp: x∊(−1,14)
b) tutaj nie mogę rozszyfrować tego logarytmu

22 mar 12:08
5-latek: Najpierw zobacz masz tam wpisz a otrzymasz a w dole Kliknij po wiecej przykladow i zapisz to
porzadnie
piszac od razu zalozenie co do przykladu a)
22 mar 12:09
Maciej:
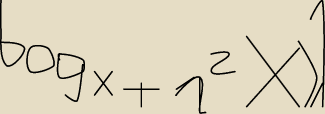
22 mar 12:14
5-latek: log(x+1)2 x≥1 ?
22 mar 12:16
Maciej: właśnie tak

przepraszam ale nie wiedziałem jak to zrobić

22 mar 12:21
Frost: log(x+1)2x≥1
zał. (x+1)2>0 ∧ (x+1)2≠1 ∧ x>0
D: x ∊ (0,+∞)
22 mar 12:22
Frost: U{1]{2}log
x+1x≥1
log
x+1x≥2
log
2x≥2log
2(x+1)
log
2x−log
2(x+1)
2≥0
x≥(x+1)
2
0≥x
2+x+1
wychodzi mi x=0 ale nie należy do dziedziny więc sprzeczność ale nie wiem czy dobrze
zrobiłem...
Masz odpowiedzi?
22 mar 12:29

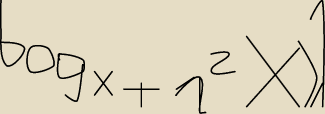
 przepraszam ale nie wiedziałem jak to zrobić
przepraszam ale nie wiedziałem jak to zrobić 