Ostrosłup przecięty płaszczyzną Szem: W ostrosłupie ABCS prawidłowym trójkątnym krawędź podstawy ma długość a. Przez wierzchołek S tego ostrosłupa i środki dwóch krawędzi podstawy poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod kątem β. Oblicz pole P otrzymanego przekroju. Bardzo proszę o wszelką pomoc!

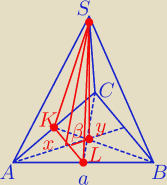
Janek191: Mamy I KL I = 0,5 a ( Tw. Talesa )

	√3
x = 0,5 a		= 0,25 √3a
	2

	1		1		√3		1
y =		hp =		a		=		a√3
	3		3		2		6

	√3		1		1		1
z = hp − x − y = a		−		a√3 −		a √3 =		a√3
	2		4		6		12

oraz

z
	= cos β
h1

	a√3{12}
U{		= cos β
	h1

	a √3
h1 =
	12 cos β

Pole przekroju

	√3 a		0,25 √3 a2
P = 0,5I KL I*h1 = 0,5* 0,5 a *		=
	12 cos β		12 cos β

	√3 a2
P =
	48 cos β

====================

Szem: Bardzo dziękuję!