Ciągi równości i nierówności mat: 1. Dla jakiej liczby α suma wyrazów nieskończonego ciągu geometrycznego (α, 3α4, 9α16, ... ) jest równa 12? 2. Dla jakiej wartości x składniki sumy 1 + x+12x+3 + (x+12x+3)2 + ... są kolejnymi wyrazami ciągu geometrycznego zbieżnego? 3. Rozwiąż równanie 1 + 11 − x + 1(1−x)2+ ... = 1 − 2x 4. Rozwiąż nierówność 1x+1 + 1(x+1)2 + 1(x+1)3 + ... ≤ 3x−2 5. Wyznacz dziedzinę funkcji f(x) = 1 + 2x+3 + 22(x+3)2 + ... a następnie: a) narysuj wykres funkcji f b) podaj zbiór wartości funkcji f. Odpowiedzi: 1. α=3 2. x ∊ (−∞, 2) ∪ (−43,+∞) 3. − √22 4. x ∊ <1,+∞) 5. f(x) = 2x+1 + 1, Df = (−∞,−5) ∪(−1,+∞) b) ZWf= (12, 1) ∪ (1, +∞) Bardzo proszę o wytłumaczenie mi tych zadań na sprawdzian. Szczególnie nie rozumiem nierówności przy założeniach i rysowania wykresów |x| < a ⇔ x<a ∩ x>−a |q|<1 S = a11−q q = a2a1

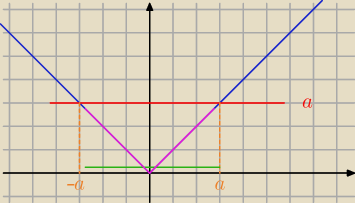
Qulka: jak widać jak |x| jest mniejszy od a (to fioletowe ) to x jest jednocześnie większy od −a i mniejszy od a (to zielone)

Qulka: |q| <1 żebyś wciąż dzieliła następne i miała coraz mniejsze liczby..żeby w nieskończoności już praktycznie nic nie przybywało i dlatego jest konkretny wynik tej sumy

Qulka:

	a1
i właśnie wtedy jak masz taki zbieżny suma wszystkich jest taką liczbą S=
	1−q

Qulka: z definicji ciągu geometrycznego każdy jest większy stałą liczbę razy czyli a₂=a₁•q a₃=a₂•q itd..

	a2
i dlatego q się nazywa ilorazem że q=
	a1

Qulka: zadanie 1 q=3/4

	a
S=		=12
	1−3/4

4a=12 a=3