 Witam,
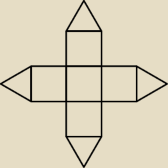
Rysunek przedstawia siatkę wielościanu. Oblicz długość jego najdłuższej przekątnej przyjmując,
że wszystkie krawędzi mają długość 1.
Mam z tym zadankiem problem. Zaraz dopiszę drugiego posta.
Witam,
Rysunek przedstawia siatkę wielościanu. Oblicz długość jego najdłuższej przekątnej przyjmując,
że wszystkie krawędzi mają długość 1.
Mam z tym zadankiem problem. Zaraz dopiszę drugiego posta.
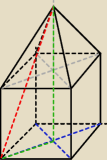 Tak mniej więcej to wygląda.
Czerwona przekątna, to ta najdłuższa, tak?
Tak mniej więcej to wygląda.
Czerwona przekątna, to ta najdłuższa, tak?
| √2 | ||
W takim razie wysokość ostrosłupa u góry to | ||
| 2 |
| √2 | ||
No i połowa przekątnej podstawy sześcianu to | ||
| 2 |
| √2 | √2 | |||
(1+ | )2+( | )2=p2 | ||
| 2 | 2 |

 Pełne polecenie mam jeszcze z kodowaniem odpowiedzi:
Zakoduj wynik podając trzy początkowe cyfry jego rozwinięcia dziesiętnego.
A odpowiedź:
to u góry
Pełne polecenie mam jeszcze z kodowaniem odpowiedzi:
Zakoduj wynik podając trzy początkowe cyfry jego rozwinięcia dziesiętnego.
A odpowiedź:
to u góry