Geometria analityczna Kamix: Pomoc pilnie potrzebna Sprawa wygląda tak, że mam bardzo dużo zajęć w ten weekend. Dostaliśmy 8 zadań do przygotowania i kolokwium będzie z 2 z tych zadań. Dlatego bardzo proszę o pomoc w rozwiązaniu, jak mówię nie są to jakieś bardzo skomplikowane zadania, ale chcę się ich nauczyć, a dopiero później wrócę się i opracuję te tematy gruntownie. Zad1: Wyznaczyć równanie płaszczyzny przechodzącej przez punkty A=(2,−1,3), B=(3,1,2) i równoległej do wektora a=[−3,1,4] Jak zrobić to zadanie?

Kamix: Ok już wpadłem na pomysł jak zrobić to zadanko Po dłuugim czasie.

Kamix: Tych zadań już chyba niestety nie rozgryzę: Zad: Wyznaczyć równanie płaszczyzny π przechodzącej przez punkt M(1,1,1) i równoległej do płaszczyzny π`:−2x+y−z+1=0. Obliczyć odległość między tymi płaszczyznami. Zad: Obliczyć objętość czworościanu ograniczonego płaszczyzną 2x+3y+6z−12=0 i płaszczyznami układu współrzędnych. Bardzo proszę o pomoc

Janek191: π₁ : − 2 x + y − z + 1 = 0 to może tak π₂ : − 2x + y − z + k = 0 i M= ( 1,1,1) należy do π₂ wstaw do jedynki i oblicz k

Janek191: Miało być : wstaw jedynki za x , y, z do −2 x + y − z + k = 0 i wyznacz k.

Kamix: Dzięki wielkie Janek Równanie tej płaszczyzny wyszło mi −2x+y−z+2=0. A jak obliczyć teraz odległość między tymi płaszczyznami?

Janek191:

	I k − k1 I		I 1 − 2 I
d =		=		=
	√ A2 + B2 + C2		√(− 2)2 + 12 +(−1)2

	1		1		√6
=		=		=
	√4 + 1 + 1		√6		6

Kamix: Ok wszystko zrozumiałe. A co z tą objętością czworościanu? Jedna płaszczyzna to jest 2x+3y+6z−12=0, druga natomiast będzie zawierała punkt P(0,0,0). I tutaj moje pomysły się niestety kończą.

AS: Objętość Przyjmij x = 0,y = 0,wylicz z otrzymasz wierzchołek na osi Oz (0,0,zo) Podobnie z pozostałymi wierzchołkami.

Kamix: A mógłbyś to jakoś rozpisać? Bo nie za bardzo wiem co z czym

AS: Nie rozpiszę − moje objaśnienie powinno wystarczyć. Powstanie ostrosłup o jednym wierzchołku w początku układu a pozostałe trzy na osiach układu. Trochę rusz głową

Kamix: Nie interpretuj tego źle, ale zależy mi przede wszystkim na czasie. Chciałbym mieć ten komfort, żeby móc pozwolić sobie na myślenie nad każdym zadaniem po godzinie. Kolokwium ma być z dwóch zadań z listy, dlatego chciałbym zobaczyć jak się je rozwiązuje, nauczyć się, spróbować zrozumieć, a gruntownie nad tym przysiądę w następny weekend.

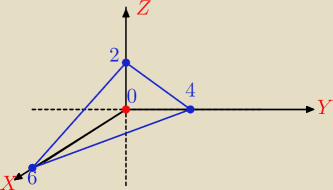
Mila: 2x+3y+6z−12=0

Kamix: Dziękuję Mila o takie wytłumaczenie mi chodziło

	1
Teraz tak, będzie to ostrosłup o podstawie trójkąta. Wzór na objętość to		Pp*h. Jak teraz
	3

policzyć długości boków tego trójkąta?

Kamix: Up...

Mila: A nie widać?,

Odpowiedzi na debilne pytania: Mila policz do końca, bo Kamix ma pilne kolokwium a nie chce mu sie za dużo główkować

Kamix: Pole podstawy wychodzi mi 2√5.

	1
Czyli objętość 2√5*		*6=4√5. Dobrze?
	3

Mila: Oczywiście ma być V _ostrosłupa.

Mila: Jako podstawę ostrosłupa możesz przyjąć Δ leżący w płaszczyźnie XOY.

	1
Pp=		*6*4=12
	2

	1
V ostrosłupa=		*12*2=8
	3

Kamix: Dziękuję Milu Przeanalizuję zadanko i myślę, że będę w stanie zrobić podobnie Mam jeszcze takie zadanko: Wykazać, że proste: l₁: x+y+z=0, 2x+y+2z=0,, l₂: x=−t y=−8 z=2+t są równoległe. Napisać równanie płaszczyzny, w której lezą proste l₁, l₂ oraz obliczyć ich odległość. Jak sprawdzić czy proste te są równoległe? Podstawiłem do równania l₁ x,y,z z równania l₂, ale po rozwiązaniu układu wyszło 0t=6 i z drugiego −t=6. Wiem, że współczynnik kierunkowy musi być taki sam ale z pierwszego wychodzi mi, że t należy do zbioru pustego...

Mila: l₁ jest podana w postaci krawędziowej, przekształcamy do postaci kierunkowej: Przyjmujemy z jako parametr: z=t x+y=−t 2x+y=−2t odejmuję stronami −x=t x=−t −t+y=−t l₁: równanie parametryczne x=−t y=0t z=t wektor kierunkowy prostej l₁: k₁^→=[−1,0,1] wektor kierunkowy prostej l₂: k₂^→=[−1,0,1] Wektory k₁ i k₂ są równoległe. ======================== Prosta l₁ przechodzi przez punkt P=(0,0,0) prosta l₂ przechodzi przez punkt Q=(0,−8,2) PQ^→[0,−8,2] n^→=PQ^→x[−1,0,1] wektor normalny szukanej płaszczyzny n^→=[0,−8,2]x[−1,0,1]=−8i−8j−8k=[−8,−2,−8] π: −8*(x−0)−2*(y−0)−8*(z−0)=0 −8x−2y−8z=0 /:(−2) π: 4x+y+4z=0 ============

Kamix: Jejku Mila dziękuję, naprawdę szczerze dziękuję A jeszcze mam pytanie, jak się oblicza kąt między prostymi, gdy obie proste podane są w postaci krawędziowej?

Hugo: Mila

Mila: Chyba trzeba znać wektor kierunkowy i z iloczynu skalarnego wyznaczamy cosinus. Zobacz do notatek.

AS: Chłopie kochany − co w końcu umiesz? Pytasz się o elementarne rzeczy,podstawowe wzory. Nie kompromituj się.

Braun: Co racja to racja, podstawowe informacje z wykładu by wystarczyły żeby rozwiązać zadanie.

Kamix: AS nikt nie zmusza Cię do pomagania... Tak się zastanawiam tylko po co Ty tu zaglądasz. Przecież na tym forum ludzie najczęściej szukają pomocy. Nie ciętych ripost. Czy ja Cie przykleiłem do tego tematu? W ogóle Cię nie rozumiem. W dodatku pisałem, że nie umiem za wiele z tego względu, że wykładów nie mieliśmy z powodu choroby wykładowcy. Dlatego dostaliśmy 8 zadań, które mamy opracować sami i z racji tego, że nie mieliśmy wykładów ani ćwiczeń, bo prowadzący jak już mówiłem chorował, ujawnił nam zadania, które będą na kolokwium. Najpierw chcę się ich pouczyć, a dopiero po kolokwium zabiorę się za temat od podstaw kompleksowo. Bo teraz nie mogę sobie na to pozwolić ze względów czasowych. Nie mam też notatek, bo nie mieliśmy żadnych zajęć, a teraz trzeba na łeb na szyję gonić stracony czas. Dlatego wygląda to jak wygląda. Chcesz pomóc to pomagasz, nie chcesz to nie pomagaj. Przecież to prosty wybór. Po co od razu komuś wbijać szpilki w czoło nie znając kompletnie okoliczności. AS − Panu już dziękujemy.

Mila: Wektor kierunkowy prostej podanej w postaci krawędziowej można wyznaczyć również tak: l₁: x+y+z=0, 2x+y+2z=0, k₁^→=[1,1,1] x [2,1,2]=i−k=[1,0,−1] masz to samo co obliczyłam inną metodą 18:29 tam masz wektor [−1,0,1] a jest on równoległy do wektora [1,0,−1]

Kamix: Metoda z 18:29 okazała się również zrozumiała Dziękuję za pomoc.

Mila:

Kamix: A jeszcze mam pytanie jak obliczyć odległość między tymi prostymi?

Mila: Wybierasz punkt który należy do jednej z tych prostych i oblicz jego odległość od tej drugiej. 1) l₁: równanie parametryczne x=−t y=0t z=t Prosta l₁ przechodzi przez punkt P(0,0,0) l₂: x=−t y=−8 z=2+t 2) Piszesz równanie płaszczyzny π⊥do obu prostych i przechodzącej przez punkt P(0,0,0)∊l₁. Wektor normalny płaszczyzny : n^→= wektorowi kierunkowemu k^→ =[1,0,−1] π: 1*(x−0)+0*(y−0)−1*(z−0)=0 π: x−z=0 3) Szukamy punktu Q przecięcia prostej l₂ z płaszczyzną π; −t−(2+t)=0 −t−2−t=0 −2t=2 t=−1 Q=(−(−1),−8,2−1)=(1,−8,1) |PQ|=√... długość tego odcinka to jest odległość tych prostych.

Kamix: Mila, nawet sobie nie wyobrażasz jak jestem Ci wdzięczny za tą bezinteresowną pomoc. Długość odcinka |PQ| wyszła mi √68. Z całej listy zostały mi jeszcze dwa zadanka, których nie bardzo potrafię sam zrobić? Czy znalazłabyś czas może wieczorkiem żeby mi pomóc. Sam też zrobiłem kilka zadanek, dlatego chciałbym Cię też prosić o fachowe zerknięcie czy rozwiązałem je poprawnie. Pierwsze zadanko z dwóch, które nie wiem jak zrobić... Obliczyć kąt między prostą l:x+y+z−2=0, 2x+y−z−1=0, a płaszczyzną wyznaczoną przez punkty A=(2,3,−1), B=(1,1,0), C=(0,−2,1).

Mila: Napisz równanie płaszczyzny. Chcę zobaczyc jak to robisz.

Mila: |PQ|=√1²+8²+1²=√66

Kamix: Tak, tak, |PQ| to blad rachunkowy, zgadza sie √66 Rownanie plaszczyzny, to wyznaczam wektor AB i AC, potem wyznaczam wektor prostopadly do plaszczyzny wykonujac dzialanie ABxAC, podstawiam do rownania plaszczyzny i wyliczam z tego D I pisze kompletne rownanie plaszczyzny. Przepraszam, ze nie posluguje sie konkretnymi liczbami, ale nie mam dostepu do laptopa tymczasowo

Mila: Kąt między prostą i płaszczyzną: 1) Wektor kierunkowy prostej l:x+y+z−2=0, 2x+y−z−1=0, k^→[1,1,1] x [2,1,−1]=[−2,3,−1] wektor kierunkowy prostej l. 2) równanie płaszczyzny π: A=(2,3,−1), B=(1,1,0), C=(0,−2,1). AB^→=[−1,−2,1] AC^→=[−2,−5,2] n^→=[−1,−2,1] x [−2,−5,2]=i+k=[1,0,1] wektor normalny płaszczyzny π π: 1*(x−2)+0*(y−3)+1*(z+1)=0⇔ x−2+z+1=0 x+z−1=0 3) Kąt między prostą a płaszczyzną:

	|k→x n→|
cosα=
	|k|*|n|

	|[−2,3,−1] x [1,0,1] |
cosα=		=
	√22+32+12*√12+12

	|[−3,−3,−3]|		√9+9+9		√27
cosα=		=		=
	√14*√2		√28		√28

Posprawdzaj sobie rachunki, bo mogłam sie pomylic.

Kamix: Chyba wszystko sie zgadza naprawde nie wiem jak Pani dziekowac... Naprawde z calego serca dziekuje zostalo mi ostatnie zadanie, gdy jutro bedzie Pani miala czas, prosze o pomoc. I podesle to co rozwiazalem sam, zeby Pani mogla spojrzex czy dobrze Bardzo dziekuje za wszystko!

Mila: Jeśli potrafię to sprawdzę ( Sporo zapomniałam). Jakoś pigor tu nie zagląda a jest bardziej na bieżąco z tym materiałem. Może mnie wesprze w sprawdzaniu. Powodzenia

kyrtap: Mila i tak jesteś mądra

AS: Mila. Według moich obliczeń,odległość między prostymi skośnymi wynosi 0. Liczona wzorem (Bronstein) daje taki sam wynik.

Mila: Witaj AS. AS wiesz gdzie popełniłam błąd? Cosinus mam bliski 1 więc gdzieś w rachunkach może mam błąd. Kamix miał sprawdzić, bo było już późno dla mnie.

Mila: AS, o które zadnie Ci chodzi, podaj godzinę.

Kamix: I ostatnie zadanie z którym nie mogę sobie poradzić, Mila pomóż. A wieczorkiem już wstawię te zadania, które sam policzyłem. Zbadać wzajemne położenie prostych l₁:2x−4y−2z=0 2x−y−z=0 l₂:x=1+t y=1−t z=3t. Z góry dziękuję za pomoc

Kamix: Mila sprawdzałem i wychodzi ok.

Mila: k¹− wektor kierunkowy prostej l₁ z=t 2x−4y=2t 2x−y=t odejmuję stronami

	−1
−3y=t⇔y=		t
	3

	−1
2x−(		t)=t
	3

	1
2x+		t=t
	3

	2
2x=		t
	3

	1
x=		t
	3

Równanie parametryczne l₁:

	1
x=		t
	3

	1
y=−		t
	3

z=t

	1		1
===== ⇔k1→=[		,−		,1] wektor równoległy do k→=[1,−1,3]
	3		3

k₂^→=[1,−1,3]⇔l₁ || l₂

AS: Wektory kierunkowe prostych: u = [−1,0,1] , v = [−1,0,1] Wektor normalny: w = u x v = [0,0,0]

Mila: As, 23 .03 g. 16:35 pisałam równanie płaszczyzny prostopadłej do obu prostych.

Kamix: Dziękuję Mila! Jeszcze wieczorkiem wstawię te zadanka rozwiązane przeze mnie, jeżeli znajdziesz chwilkę to zerknij. Nawet nie wiesz jak dziękuję za Twoją dotychczasową pomoc.

Mila: