Oblicz objętość graniastosłupa prawidłowego czworokatnego xxx basia xxx: Przekątna graniastosłupa prawidłowego czworokątnego ma długość 20 cm i jest nachylona do płaszczyzny podstawy pod kątem 30 stopni. Oblicz objętość tego graniastosłupa.

xxx basia xxx: Pomocy

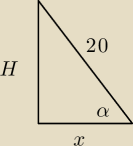
J: x − przekątna podstawy, policz x i H

H
	= tgα
x

H² + x² = 20² x = a√2 , gdzie a to krawędź podstawy

xxx basia xxx: Jak to policzyć ?

J:

	√3
H =		x
	3

	√3
(		x)2 + x2 = 400
	3

xxx basia xxx: D=20 sin30^o = \frac{h}{D}\\ \frac{1}{2}=\frac{h}{20}\\ h=10 cos30^o = \frac{d_p}{D}\\ \frac{\sqrt{3}}{2} = \frac{d_p}{20}\\ d_p=10\sqrt{3} d_p=a\sqrt{2} \Rightarrow 10\sqrt{3} = a\sqrt{2} \Rightarrow a=5\sqrt{6} V=a² \cdot h = (5\sqrt{6})² \cdot 10 = 1500 \ cm³ P_pc = 2a² + 4ah = 2(5\sqrt{6})² + 4\cdot 5\sqrt{6} \cdot 10 = 300 + 200\sqrt{6} = 100(3+2\sqrt{5}) \ cm

xxx basia xxx: D=20 sin30^o = \frac{h}{D}\\ \frac{1}{2}=\frac{h}{20}\\ h=10 cos30^o = \frac{d_p}{D}\\ \frac{\sqrt{3}}{2} = \frac{d_p}{20}\\ d_p=10\sqrt{3} d_p=a\sqrt{2} \Rightarrow 10\sqrt{3} = a\sqrt{2} \Rightarrow a=5\sqrt{6} V=a² \cdot h = (5\sqrt{6})² \cdot 10 = 1500 \ cm³ P_pc = 2a² + 4ah = 2(5\sqrt{6})² + 4\cdot 5\sqrt{6} \cdot 10 = 300 + 200\sqrt{6} = 100(3+2\sqrt{5}) \ cm

J: x = 10√3