Wektory równoległobok M: Punkt S (1,0) jest środkiem boku ab równoległoboku ABCD. Wyznacz współrzędne wierzchołków tego równoległoboku oraz oblicz jego pole, jeżeli (wektor) BC =[1,3] i (wektor) CD =[−6,−2]

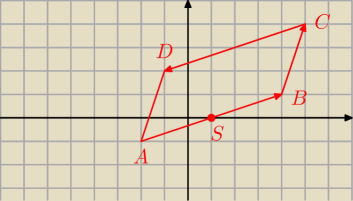
Janek191: S = ( 1, 0) A = ( a , b) B = (c, d) C = ( e ,f)

a + c		b + d
	= 1		= 0
2		2

więc a + c = 2 b + d = 0 → → AB = − CD = − [ − 6 , −2 ] = [ 6, 2] więc → AS = 0,5* { 6 , 2 ] = [ 3, 1] [ 1 − a, 0 − b ] = [ 3, 1 ] 1 − a = 3 i − b = 1 a = − 2 b = − 1 A = ( − 2, − 1) ========== → SB = 0,5*[ 6, 2] = [ 3. 1] [ c − 1, d − 0] = [ 3 , 1] c = 4 i d = 1 B = ( 4, 1 ) ======== → BC = [ 1 , 3] więc C = ( 4 + 1 , 1 + 3) = ( 5, 4 ) ==================== → CD = [ − 6 , − 2 ] więc D = ( 5 − 6, 4 − 2 ) = ( − 1, 2) ===================== [

Janek191: → AB = [ 6, 2 ] → → AD = BC = [ 1 ,3 ] więc pole równoległoboku jest równe → → P = I det ( AB , AD ) I = I 6*3 − 2*1 I = I 18 − 2 I = 16 ========================================