f. kwadratowa
mikejjla: Dla jakich wartości parametru m dwa różne pierwistki równania −2x
2 + mx −2m = 0 są wieksze od
1?
Moje rozwiązanie:
I.
Δ>0
m
2−16m>0
m(m−16)>0
m=0 m=16
m∊(−
∞,0)∪(16,
∞)
II.
| ⎧ | (x1−1)(x2−1)>0 | |
| ⎩ | (x1−1)+(x2−1)>0 |
|
| ⎧ | x1x2−x1−x2+1>0 | |
| ⎩ | x1+x2−2>0 |
|
| ⎧ | x1x2−(x1+x2)+1>0 | |
| ⎩ | x1+x2−2>0 |
|
| | m | | m | |
1. m− |
| +1>0 /*2 2. |
| −2>0 /*2 |
| | 2 | | 2 | |
2m−m+2>0 m−4>0
m>−2 m>4
m∊(4,
∞)
Po uwzględnieniu I założenia m∊(16,
∞)
Czy to zadanie jest dobrze zrobione? Proszę o sprawdzenie.
Szukałam rozwiązania na innych stronach i gdzieś było napisane, że z tego układu równań powinno
wyjść m>0 i m>0, więc nie wiem czy czasem nie zrobiłam gdzieś jakiegoś błędu

21 mar 11:09
J:
zrób tak:
1) Δ > 0
2) xw > 1
3) f(1) > 0
21 mar 11:14
mikejjla: czemu?
21 mar 11:17
===:
zrobiłbym to tak
2) xw>1
3) f(1)<0
Zatem:
2) m/4>1 ⇒ m>4
3) −2+m−2m<0 ⇒ m>−2
i wszystko jasne
21 mar 11:20
J:
tak ... nie zauważyłem,że a = −2
2) f(1) < 0
21 mar 11:22
J:
1) Δ > 0
2) xw > 1
3) f(1) < 0
21 mar 11:23
J:
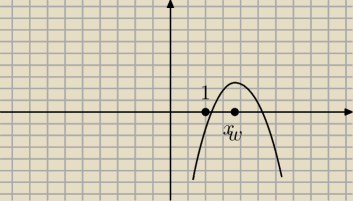
21 mar 11:26
mikejjla: Dziękuję, szczególnie za rysunek, teraz jest lepiej widoczne

21 mar 11:31


