planimetria YushokU: Witam, Mam problem z zadankiem. Nie wiem za bardzo czego się złapać.

	AD		1
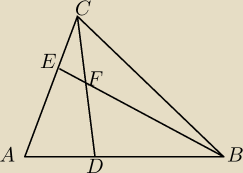
W trójkącie ABC punkty D i E leżą odpowiednio na bokach AB I AC, tak, że		=		oraz
	DB		2

	EC		EF		1
		={1}{2}. Udowodnij, że		=		.
	AE		FB		6

	1
Jedyne co udowodniłem, to, że pola ADEF i BCF są równe i PDFB=PECF+		PABC
	3

Proszę o pomoc, wskazówki, jak się za to zabrać

Qulka: może być dookoła

YushokU: może być

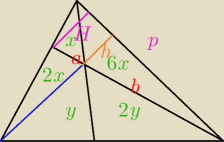
Qulka: Hp/2=7x hp/2=6x zatem H/h =7/6 =(a+b)/b

Qulka: bo 2• pole ADC = pole DBC więc 2•(3x+y) = P(CFB)+2y dlatego Pole CFB = 6x

Qulka: wszystko jasne? bo idę spać

YushokU: chyba tak, muszę to przetrawić. Dobranoc i kolorowych snów

YushokU: Dobra, fakt. Tak właśnie myślałem, że tu trzeba twierdzenia Cevy użyć, ale chciałem "maturalnie", a tak na prawdę sprowadziło się to do Cevy na około

Qulka: nie zauważyłam.. liczyłam z samych pól, a że wysokość mi przypadkowo wyszła na jednej prostej to przypadek

Qulka: niebieska, bo chciałam mieć tę samą wysokość do liczenia pola trójkącika

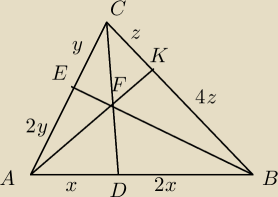
YushokU: A właściwie najprościej to chyba Cevy+von Aubel. Raz poznałem te twierdzenia przypadkiem i się okazuje, że całkiem przydatne chyba na maturze mogą być twierdzenie Cevy:

y		x		BK
	*		*		=1
2y		2x		KC

	BK		4
po wyliczeniu		=		→oznaczam na rysunku
	KC		1

twierdzenie von Aubel'a:

BF		4z		2x		6
	=		+		=
FE		z		x		1

Koniec. Ładne, przynajmniej dla mnie.

YushokU: Dziękuję Qulko, już rozumiem to zadanie