nierówności
Bartek: Mam problem z taką nierównością: −x3+5x2−11x+6>0
20 mar 21:06
20 mar 21:22
20 mar 21:23
5-latek: O ciez w morde

20 mar 21:26
Bartek: i co teraz ?

20 mar 22:37
Qulka: nic

masz rozwiązane w linku

możesz przepisać

20 mar 22:38
Bartek: No to tak jakby nie miało miejsc zerowych czy jak ?

20 mar 22:41
Qulka: ma miejsce zerowe x≈0,777505 i wszystkie x mniejsze spełniają nierówność
20 mar 22:45
Bartek: Kurde, jak można na maturze dawać takie przykłady..
20 mar 22:46
Qulka: może błąd w druku

albo w przepisywaniu

20 mar 22:46
Bartek: | | x−1 | |
W takiej postaci było |
| >x−1 sprawdzam już 5 raz i chyba dobrze wszystko  Jest to |
| | x−2 | |
jeden z przypadków w nierówności z wartością bezwzględną
20 mar 22:49
Qulka: przenosisz na jedną stronę i do wspólnego mianownika
| (x−1)(1−(x−2)) | |
| >0 //•M2 |
| x−2 | |
(x−1)(3−x)(x−2)>0 i wężyk
20 mar 22:56
Qulka:
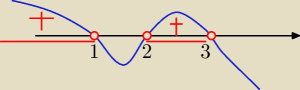
20 mar 22:57
Bartek: a jak robiłem tak, że mnożyłem przez mianownik x−2 podniesiony do kwadratu to zły sposób ?
20 mar 23:00
Bartek: bo nie wiem czy w poprzednich dwóch przypadkach dobrze robiłem mnożąc przez kwadrat mianownika

20 mar 23:04
20 mar 23:08
Benny: Nie sprawdzałem dokładnie przykładu, ale jeżeli mnożysz nierówność przez wyrażenie do kwadratu
to zwrotu nie zmieniasz

20 mar 23:09
Qulka: to nie dotyczyło, poprzedniego czyli że to nie jest zły sposób

20 mar 23:09
Qulka: właśnie po to kwadrat żeby nie zmieniać znaku nierówności
20 mar 23:10
Benny: ponieważ dla każdego a∊R a
2≥0

20 mar 23:12
Qulka: ponieważ a jest w mianowniku i M≠0 więc dla każdego M M2>0
20 mar 23:16
Benny: a przepraszam, nie doczytałem

20 mar 23:23
 http://www.wolframalpha.com/input/?i=%E2%88%92x3%2B5x2%E2%88%9211x%2B6%3E0
http://www.wolframalpha.com/input/?i=%E2%88%92x3%2B5x2%E2%88%9211x%2B6%3E0


 masz rozwiązane w linku
masz rozwiązane w linku  możesz przepisać
możesz przepisać 

 albo w przepisywaniu
albo w przepisywaniu 
 Jest to
Jest to

 ale potem masz x3 i szukasz pierwiastków i robisz głupie błędy
x2−3x+2>x3−5x2+8x−4 więc −x3+6x2 −11x+6>0
http://www.wolframalpha.com/input/?i=%E2%88%92x3%2B6x2%E2%88%9211x%2B6%3E0
ale potem masz x3 i szukasz pierwiastków i robisz głupie błędy
x2−3x+2>x3−5x2+8x−4 więc −x3+6x2 −11x+6>0
http://www.wolframalpha.com/input/?i=%E2%88%92x3%2B6x2%E2%88%9211x%2B6%3E0



