Prawdopodobieństwo Patryk: W urnie I jest 5 białych kul i 7 czarnych kul, w urnie II są 2 białe kule i 3 czarne kule. Wyjmujemy dwie kule z I urny i dokładamy do II urny, a następnie z II urny wyjmuje jedną kulę. Oblicz prawdopodobieństwo, ze po dołożeniu kul wyjmujemy z II urny kulę czarną. W kluczu są rozpisane przypadki, ale bez konkretnych szczegółów. Mógłby ktoś rozrysować drzewko dwuetapowe uwzględniające wszystkie przypadki? Bo nie wiem nawet jak takie drzewo może wyglądać − nigdy nie używałem drzewka, a tutaj chyba jest to najlepszy sposób.

Patryk: Wyliczyłem:

	10
1. Gdy wylosujemy 2 kule białe z 1 urny (P(bb)=		), to prawdopodobieństwo wyjęcia kuli
	66

	3
czarnej z 2 urny wynosi
	7

	21
2. Gdy wylosujemy 2 kule czarne z 1 urny (P(cc)=		), to prawdopodobieństwo wyjęcia kuli
	66

	5
czarnej z 2 urny wynosi
	7

	35
3. Gdy wylosujemy 1 kule białą i 1 kulę czarną z 1 urny (P(bc)=		), to
	66

	4
prawdopodobieństwo wyjęcia kuli czarnej z 2 urny wynosi
	7

Ale nie wiem jak to "scalić" w ogólne prawdopodobieństwo

Qulka:

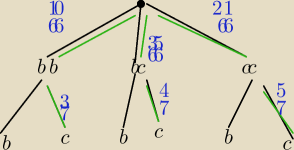
	10		3		35		4		21		5
P(czarna) =		•		+		•		+		•		= ...
	66		7		66		7		66		7

idziesz po zielonych gałązkach w dół mnożysz w bok dodajesz

Patryk:

	275
Hmmm, czyli P(czarna)=		− mi tez tak wychodziło, a w kluczu jest
	462

	187
P(czarna)=		, czyli błąd?
	462

Patryk:

	2
Raczej błąd, bo patrzę wyżej, to jedna "gałązka" wynosi		, czyli policzone dla białej
	7

kuli. Dzięki Qulka!