parametr whatnot: wyznacz k dla którego dziedziną funkcji f(x) = √(1−k²)x² + (k−1)x +1 jest zbiór liczb rzeczywistych.

5-latek: 1. 1−k²>0 2 Δ≤0 rozwiaz te dwa warunki

whatnot: tak sie zastanawialem wlasnie, a nie wystarczyłoby ze 1−k² różne od zera i Δ≤0?

Metis: Wystarczyłoby

Metis: Z resztą warunek: x≠0 jest koniecznym skoro Δ≤0.

whatnot: no tak, ale jest jeszcze z drugiej strony tez to, ze wyraenie pod pierwiastkiem musi byc dodatnie, co wskazywałoby na dodatni współczynnik a xd

5-latek: ale √0= 0 czyli istnieje

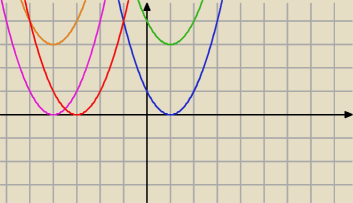
Mila: 1) 1−k²=0⇔k=1 lub k=−1 wtedy : dla k=1 f(x)=√(1−1)x²+(1−1)x+1=√1 =1 dla każdego x∊R dla k=−1 f(x)=√(1−1)x²−2x+1=√−2x+1

	1
wyrażenie −2x+1 przyjmuje wartości ujemne i f(x) jest określona tylko dla x≤
	2

2) (1−k²)>0 i Δ≤0 oznacza, że f(x) przyjmuje tylko wartości nieujemne . Przykładowe wykresy funkcji podpierwiastkowej .

Metis: Dobrze, że czuwasz