Wyznacz liczbę pierwiastków równania w zależności od parametru m. several27: Mam problem z takim zadankiem: Wyznacz liczbę pierwiastków równania w zależności od parametru m:

2x2
	=m
x2+4x+4

Obliczyłem pochodną, wyszło mi że (−2, undef) − max, (0,0) − min. Wszystko wiem jak zrobić oprócz wyznaczenia poziomej asymptoty (które jest równa 2) tylko dla jednej części wykresu, dla pierwszego ramienia od lewej. Dlaczego działa ona tylko na część funkcji. (wiem to z wykresu kalkulatora, ale nie wiem jak do tego samemu dojść).

Dziadek Mróz: Krzem, Fosfor i Miedź

stonoga: 2x²=mx²+4xm+4m 2x²−mx²−4xm−4m=0 (2−m)x²−4xm−4m=0 Δ=(−4m)²−4(−4m)(2−m)=16m²+16m(2−m)=16m²+32m−16m²=32m 32m>0 m>0 dwa pierwiastki rzeczywiste dla m>0 32m=0 m=0 jeden pierwiastek rzeczywisty dla m=0 32m<0 m<0 żadnych pierwiastków rzeczywistych dla m<0

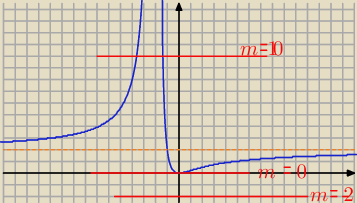
Qulka: dla m<0 brak pierwiastków dla m=0 lub m=2 jeden pierwiastek dla m∊(0;2)u(2;∞) dwa pierwiastki

silly goose: Skąd mam wiedzieć jak narysować tę funkcje albo jak poprawnie ją policzyć?

ite: a umiesz już badać przebieg zmienności funkcji?

ICSP: Umie. 20 mar 17:29 napisał, że policzył pochodną. Wie zatem jak badać przebieg zmienności.

chichi: (2−m)x²−4mx−4m=0 Przypadek liniowy: m=2 −8m−8=0 ⇒ x=−1 − 1 rozw. Zauważmy, że dla m=0 zerują się wyrazy: z x¹ oraz wyraz wolny, zatem mamy: 2x²=0 ⇒ x=0 − 1 rozw. A dwa rozwiązania wyznacz sobie z delty i na koniec uwzględnij to co wyżej

ite: ICSP kto inny 20 mar 2015 17:29 napisał, że policzył pochodną, a kto inny dzisiaj pyta : )

ICSP: Faktycznie