współrzedne całkowite Paulina : Udowodnij, że jedynym punktem o obu współrzędnych całkowitych, należacym do krzywej o równaniu y=√2x²−8√2x+16√2−2 jest punkt P=(4,2)

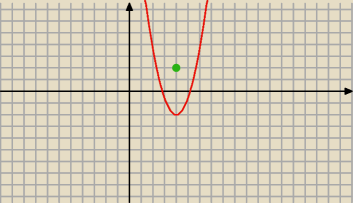
5-latek: To jest wykres tej funkcji jak widzisz punkt P=(4,2) nie nalezy do wykresu tej funkcji jesli chcesz sprawdzic to wykonaj obliczenia 2= √2*4²−8√2*4+16√2−2

Paulina : przepraszam, w treści jest P=(4,−2) taki efekt robienia matematyki w piątek wieczorem

5-latek: Sprawa ogolnie przdstawia sie tak ; jesli dany punkt nalezy do wykresu funkcji oznacza to ze wspolrzedne danego punktu spelniaja to rownanie czyli do rownania funkcji za y podstawiasz wspolrzedna y_kowa punktu a za x wspolrzedna x_owa punktu Wiec sprawdz czy to prawda −2= 2*√2*4²−8√2*4+16√2−2 jesli tak to ten punkt jest jednyn z takich punktow o calkowitych wspolrzednych (ale nie jedynym Popatrz na wykres i zobacz z eto rownanie spelnia rpwniez punkt o wspolrzednych (2,4) i punkt o wspolrzednych (6,4)

Paulina : rzeczywiście, czyli zadanie jest źle sformułowane ?

5-latek: Jesli taka tresc to zle ale Ty masz zbadac czy ten punkt nalezy do wykresu tej funkcji Zrobilas juz to?

Paulina : daje nam coś zapisanie równia w postaci √2(x−4)²−2 ?

Paulina : po podstawieniu wychodzi, że należy

5-latek: Post 17:58 to ladnie zapisany wzor tej funkcji w postaci kanonicznej Oczywiscie ze da −2= √2(4−4)²−2

Paulina : i wtedy chyba juz widoczne jest ze całowiete współrzedne beda tylko gdy x=4, tak?

5-latek: tak Ale mala uwaga : Punkt posiada dwie wspolrzedne Wiec punkt P=(4,−2) jest punktem o obu wspolrzednych calkowitych Zle odczytalem z tamtego wykresu punkty zamiast (6,3) to (6,4) i zamiast (2,3) to (2,4) teraz jak policzylem np czy punkt A=(6,3) nalezy to 3= √2(6−4)²−2 to 3=4√2−2 a to nie jest prawda Wiec na tamtym wykresie byla za mala rozdzielczosc i wprowadzila w blad . wiec Tresc zadania jest OK .

5-latek: Czas zmienic okulary

Paulina: Ale zadanie wyszlo, dziekuje