trapez pudel i hanecka: W trapezie ABCD(|AB|>|CD|) przekątna AC jest podzielona w stosunku

	|OC|
takim że		=k(O−punkt przecięcia się przekątnych trapezu)
	|AC|

Policz to k jeśli wiadomo że S_AOD=6,a S_ABCD=25

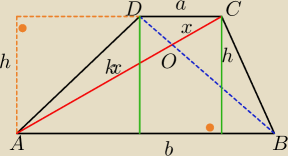
Frost: |OC|=k*|AC| P_ABCD=25 P_AOD=6

	ah
6=
	2

	(a+b)*h
25=
	2

Janek191:

a*h
	− pole Δ ACD , a nie pole Δ AOD
2

Miłosz: Proust namalował nam piękny rysunek,którego nie powstydziła by się nawet tablica na katedrze i wypisał dwa niewątpliwie poprawne

	x
wzory.Z tym że jeśli oznaczył |OC|=x to |AC|=		.Ale oczywiście
	k

zadanie pozostało nie rozwiązane.Idąc tym tropem ja bym proponował rozwiązać na k poniższy układ równań:

a
	=k ⋀ 2SAOD+abSAOD+baSAOD = SABCD
a+b

Eta:

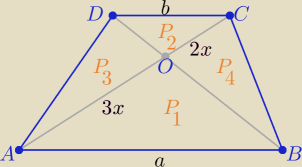
	|AO|
|AB|>|CD| to trójkąty ABO i CDO są podobne w skali p=
	|OC|

P₃=P₄=6 i P₃=√P₁*P₂ ⇒ P₁*P₂=36 P(trapezu)=25 ⇒P₁+12+P₂=25 ⇒ P₁+P₂=13

	3
to P1=9 i P2=4 ⇒ p=		⇒ |AO|=3x , |OC|=2x, |AC|=5x, x>0
	2

	2x		2
zatem k=		⇒ k=
	5x		5

Eta: Pudel z Hanecką coś długo spacerują

pudel i hanecka: Trzeba sie przewietrzyć.Ale "spasiba" wam wszystkim za pomoc