optymalizacja trapez wpisany w okrąg Damsel in Distress: Rozpatrujemy wszystkie trapezy, wpisane w okrąg o promieniu 12 w taki sposób, że podstawa trapezu jest średnicą okręgu. Oblicz długości boków tego z rozpatrywanych trapezów, który ma największe pole. Męczę się z tym zadaniem od dłuższego czasu. Nieustannie wychodzi mi we wzorze różnica pierwiastków. Podobno wykorzystując przekątną trapezu opartą na średnicy da się ułożyć 3 równania, z których następnie można wydobyć wysokość, ale tego nie widzę. Albo inaczej, nic konkretnego z tego nie wychodzi. Bardzo proszę o pomoc.

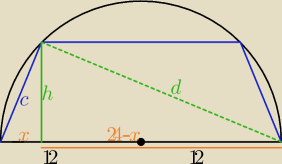
Qulka: można 3 Pitgorasy jak koniecznie chcesz h²+x²=c² c²+d²=24² d²+(24−x)²=d²

Qulka: ale chyba szybciej jest jako zmienną wziąć kąt α między c a x

Damsel in Distress: tylko że wówczas musiałabym robić pochodną z funkcji trygonometrycznej, tak jest?

Qulka: pochodne z funkcji trygonometrycznych są bardzo miłe

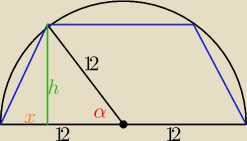
Qulka: ale chyba lepszy będzie ten kąt α i wtedy pole P= (12+12cosα)•12sinα = 144(1+cosα)sinα

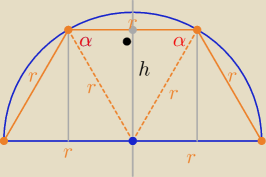
Eta: α=60^o największe pole ma trapez złożony z trzech trójkątów równobocznych o boku "r" : P= 3*P(trójkąta równobocznego)

Damsel in Distress: podobno są, z tymże nie ma ich niestety w programie liceum dlatego, jeżeli byłaby taka możliwość, to prosiłabym o inną wskazówkę

Damsel in Distress: Eta, pewnie jest tak jak mówisz, ale jak do tego dojść?

Eta: Tak jak radzi Qulka P(α)=144(1+cosα)*sinα (cosα)^'= −sinα , (sinα)^'=cosα P^'(α)= 144(−sinα*sinα+(1+cosα)*cosα) P^'(α)=0 −sin²α+cos²α+cosα=0 ⇒ −1+cos²α+cos²α+cosα=0 2cos^'α+cosα−1=0 Δ =9

	−1+3		1		−1−3
cosα=		=		v cosα=		=−1 −−− odrzucamy
	4		2		4

α= 60^o i dokończ..............

Qulka: jak nie ma w programie to tak ciężko przeczytać że pochodną sinα jest cosα albo że pochodną cos jest −sin

Damsel in Distress: Kurczę nie jest to trudne, ale nie o to chodzi. Po prostu chcę to rozwiązać innym sposobem, ponieważ wg nauczyciela się da. W każdym bądź razie i tak dziękuje za pomoc

Qulka: da się ..tylko muszę sobie przypomnieć, bo te kąty są tak wygodne że już nie pamiętam jak rozwiązywałam kiedyś

Qulka: i będą wtedy pierwiastki P=(24−x)•h oraz h²+(12−x)² = 12² więc P=(24−x)•√24x−x² i pochodna