geometria Geometrykz: W trójkącie ABC, w którym A(−2, −2) oraz B(4,4), kąt przy wierzchołku B jest rozwarty. Bok AC zawiera się w prostej k:x−3y−4=0. Środek okręgu opisanego na trójkącie ABC znajduje się w odległości √10 od boku AC. Wyznacz równanie tego okręgu. mam:

	1		4
k: y=		x−
	3		3

	1		4
C(x,		x−		)
	3		3

prostopadła do k − l: y= −3x+b zgaduję, że do tej prostopadłej należy środek okręgu, w odległości √10 o prostej k − dobrze mówię? proszę o minimalną wskazówkę, nie chcę odpowiedzi − tylko lekką podpowiedź, nie chcę odpowiedzi/całego rozwiązania.

geometrykz: to chociaż odpowiedź na pytanie

Eta: Podpowiedź środek okręgu opisanego na tym trójkącie leży poniżej prostej AC( bo trójkąt rozwartokątny) symetralne boków AB i AC wyznaczają środek okręgu S(x,y) i R²= |AS|² 1/napisz równanie symetralnej boku AB 2/ skorzystaj z odległości punktu S od prostej AC −− otrzymasz równanie prostej na której leży punkt S ( uwzględnij tę prostą,która leży pod prostą AC 3/ rozwiąż układ równań prostych 1/ i 2/ otrzymasz S(...., ...) 4/ R²=|AS|²=.... 5/ napisz równanie tego okręgu ....... Powodzenia

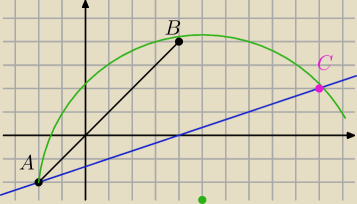
Qulka: znów nie zmieściło mi się

Eta: I zgadza się Quleczko o: (x+3)²+(y−5)²=50

geometrykz: o kurczę, wybaczcie mi, proszę, nieobecność. już się biorę!

geometrykz: (x−5)²+(y+3)²=50 dzięki!

Eta: Jasne u mnie wkradł się chochlik ( sorry) o: (x−5)³=2+(y+3)²=50

Eta: I znów chochlik wrrr o: (x−5)²+(y+3)²=50