. Norberto:

sin(90−α)*tg132*cos312
cos(180+α)sin222*ctg48

Ale jak obliczyć takie liczby jak 48,312 ?

5-latek: ctg48 nalezy do 1 cwairtji wiec go nie redukujesz natomiast zrob redukcje tg132 do kata 1 cwaiartki i zobacz co dostaniesz cos312^o= albo = cos(360−48)= zobacz na wzory albo cos(270+42)= sin 222= sin(180+44)= ... sin(90−x)= cosx cos(180+x)= zobacz soobie na wzory

Mariusz: cos(48)=cos(30+18) sin(18) możesz obliczyć albo geometrycznie albo algebraicznie , cos(18) z jedynki trygonometrycznej Jeśli argument w stopniach jest podzielny przez 3 to funkcje trygonometryczne da się ładnie zapisać

J: na czym polega geometryczna metoda obliczania sin18⁰ ?

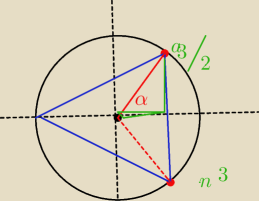
5-latek: No np na tym jesli przyjmiemy za ramie poczatkowe kąta promien dzielacy na polowy bok n−kata foremnego

	an		pi
wpisanego w kolo o promieniu R=1 to wowczas		bedzie linia sinusa kąta
	2		n

	pi		an
wiec sin		=		gdzie an to bok wielokąta foremnego
	n		2

	√5−1
a10=		(to wiemy lub przynajmnie powinnismy znac z geometrii
	2