bezwzgledna ObaMa: Wyznacz największą liczbę całkowitą spełniającą nierówność |0,01x − 2| + |0,01x − 2,5| < 0,62 Zakoduj liczbe setek dziesiatek i jednosci otrzymanego wyniku wiem mniej więcej o co chodzi, ale nie za bardzo rozumiem w jakich przedziałach to liczę : / Wiem, że mogą być na pewno 3 przypadki: −(0,01x − 2) + (−(0,01x − 2,5)) < 0,62 (0,01x − 2) + (−(0,01x − 2,5)) < 0,62 (0,01x − 2) + (0,01x − 2,5) < 0,62 nie wiem czy taki też nie może być −(0,01x − 2) + (0,01x − 2,5) < 0,62

Qulka: mógłbyś to sobie pomnożyć obustronnie przez 100 łatwiej się czyta całkowite

J: x∊ (−∞,200) U <200,+∞)

Qulka: nie może być x jednocześnie mniejszy od 2 i większy od 2,5

J: nie zauważyłem: 2,5

J: x ∊ (−∞,200) U <200,250) U <250,+∞)

ObaMa: |0,01x − 2| + |0,01x − 2,5| < 0,62 \*100 |x−2| + |x−2,5| < 6,2 faktycznie przyjaźniej wygląda Co do tych przedziałów to nadal nie do końca wiem skąd się biorą i czy może być to czwarte równanie

ObaMa: * |x−200| + |x−250| < 6,2

Qulka: największa całkowita to chyba 255

Qulka: |x−200| + |x−250| < 62

ObaMa: Tak mówi odpowiedź, ale chcę nauczyć się też sam rozwiązywać

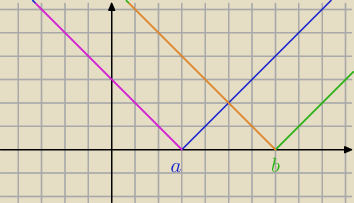
Qulka: przedziały borą się stąd że dla x<a fioletowa jest odbiciem niebieskiej więc zamiast moduł piszesz −() dla x>a jest niebieska więc moduł po prostu znika dla x<b żółtajest odbiciem zielonejwięc zamiast moduł piszesz −() dla x>b jest zielona więc moduł po prostu znika i masz 3 obszary x<a obie na minusie a<x<b jedna minus druga plus x>b obie na plusie

Qulka: nie uzyskasz przypadku x<a i jednocześnie x>b więc nie masz czwartego przypadku i do każdego przypadku koniecznie trzeba dopisać dziedzinę czyli dla jakich x jest ten przypadek żeby potem z tą dziedziną koniecznie sprawdzić odpowiedź

ObaMa: czyli: x−200 < 0 x < 200 i x−250 < 0 x < 250 i będzie x ∊ (−∞,200) −(x−200) + (−(x−250)) < 62 x ∊ (200,250) (x−200) + (−(x−250)) < 62 x ∊ (250,∞) (x−200) + (x−250) < 62 ?

J: Tak

ObaMa: A ty napisałeś : x ∊ (−∞,200) U <200,250) U <250,+∞) Czemu domknięte nawiasy

Qulka: bo tam gdzie jest większe powinno być ≥

J: IxI = a ,gdy: a ≥ 0 = −a ,gdy: a <0

Qulka: bo przy zerze nie ma znaku więc zalicza się go do tych bez zmiany znaku .. zapomniałam wstawić

Qulka: chciałam przekazać ideę przedziałów, a nie niuanse przy zerze

J: ( ... ) U < ...) U <.... ) lub ( ....> U (...> U (......) wychodzi na to samo, byleby obejmował całe R

ObaMa: Oki dzięki za wytłumaczenie, w końcu to zrozumiałem

5-latek: A do ulamkow tez sie przyzwyczajaj . Bo co zrobisz na maturze jak beda Bedziesz pisal odwolanie do CKE bo dali ulamki