Zmienne Losowe
Karpiu: Zmienna Losowa X podlega rozkładowi normalnemu o wartości oczekiwanej 2 i odchyleniu
standardowemu 3. Podaj wzór na gęstość oraz wykonaj rysunek tej gęstości.
Ktoś wie jak to zrobić?
19 mar 12:55
stonoga: wzór na funkcję gęstości rozkładu normalnego
| | 1 | | (x − μ)2 | |
f(x) = |
| e( − |
| ) |
| | √2πσ | | 2σ2 | |
| | (x − μ)2 | |
(e do potęgi ( − |
| )) |
| | 2σ2 | |
μ − wartość oczekiwana zmiennej
σ − odchylenie standardowe zmiennej
Aby wyznaczyć gęstość prawdopodobieństwa w rozkładzie normalnym dla danego wyniku należy do
wzoru podstawić wartość oczekiwaną i odchylenie standardowe dla zmiennej oraz dany wynik.
19 mar 13:25
stonoga: | | 1 | | 1 | |
we wzorze powinno być |
| lub ( |
| ) |
| | σ√2π | | √2πσ2 | |
19 mar 13:36
stonoga: teraz podstaw za σ = 3, μ = 2
19 mar 13:37
stonoga:
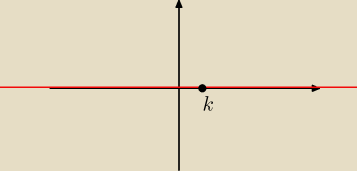
k oznacza punkt (2 ; 0,01)
19 mar 14:04
Karpiu: f(x) = 1σ √2π e −(x−2)236
19 mar 14:08
Karpiu: a dlaczego na rysunku jest punkt (2 ; 0,01) skąd to jest?
19 mar 14:12
stonoga: Jak podstawisz do wzoru za x=2 przy σ=3 i μ = 2 to f(x) = 0,01, pi w przybliżeniu i e w
przybliżeniu
19 mar 14:59
Karpiu: czyli f(x)=
13√2*3,14 2,71
−(2−2)236 = 0,01 tak

19 mar 15:08
stonoga: | | 1 | | −(x−2)2 | | 1 | | −(x−2)2 | |
f(x) = |
| e |
| = |
| e |
| |
| | 3√2π | | 2 * 32 | | 3√2π | | 18 | |
| | −(x−2)2 | |
oczywiście e do potęgi |
| |
| | 18 | |
19 mar 15:08
Karpiu: aa 18 racja
19 mar 15:09
Karpiu: ale to f(x) wychodzi wtedy 0,133
19 mar 15:10
stonoga: w mianowniku zamiast 36 to 18 i π też pod pierwiastkiem
19 mar 15:21
Karpiu: no tak i licząc na kalkulatorze wynikiem jest 0,132

19 mar 15:22
stonoga: tak powinno być (2 ; 0,13) i to jest ekstremum
19 mar 15:36
Karpiu: okej dzięki Ci

19 mar 15:37
stonoga: 0,1329787........

19 mar 15:38
Karpiu:
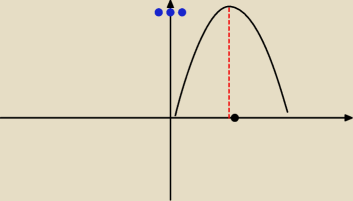
19 mar 15:42
Karpiu: patrz zakładając że tam gdzie są niebieskie kropki jest punkt 0.13 a gdzie czarna jest 2
to ten rysunek tak wygląda mniej więcej?
19 mar 15:42
Karpiu: Bo jak na Egzaminie jej taki płaski narysuje to raczej się jej to nie spodoba ^^
19 mar 15:43
 k oznacza punkt (2 ; 0,01)
k oznacza punkt (2 ; 0,01)




