Nierówność kwadratowa propeller: 4m²−55<0

J:

	55		55		55
4m2 < 55 ⇔ m2 <		⇔ −		< m <
	4		4		4

propeller: No właśnie myślałam, że tak nie można. Nie wiem czemu, ale pamiętam, że nasza nauczycielka złapała się za głowę i kazała wracać do ławki komuś, kto w taki sposób rozwiązywał podobną nierówność. Więc nie rozumiem... To dobry sposób czy nie?

J:

	55		55
tam mają być pierwiastki: − √		< m < √
	4		4

propeller: To był taki przykład: 16m²−4>0 Pani kazała rozbić tak: (4m−2)(4m+2)>0 i dopiero podać pierwiastki Nie rozumiem dlaczego się zgodziła się na 16m²>4

J: może nauczycielkę bolała głowa ..

propeller: nie zgodziła się*

propeller: Czyli można tak robić? Zawsze krzyczy "Broń Boże" kiedy ktoś w taki sposób zabiera się do rozwiązywania nierówności, więc już sama nie wiem

J: a to już "inna para butów" ... ale nie ma powodu łapać się za głowę..

	1		1		1
⇔ 16m2 > 4 ⇔ m2 >		⇔ x >		lub x < −
	4		2		2

propeller: Czemu "inna para butów"? Rozumiem, że można zastosować wzór skróconego mnożenia, ale przecież jeśli się przeniesie 4 na drugą stronę to też wyjdzie dobra odpowiedź. Właśnie zawsze się zastanawiałam o co jej chodzi, może, że na maturze tego nie zaliczają czy coś, nie wiem, ale jest tak przewrażliwiona na tym punkcie, jakby ktoś co najmniej liczył pierwiastki z ujemnej delty

J: dla świętego spokoju: 4m² − 55 < 0 ⇔ (2m −√55)(2m + √55) < 0

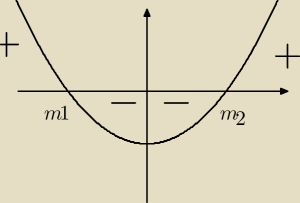
aniank: 4m²−55<0 4m²=55 m²=⁵⁵₄ m₁=− √⁵⁵₄ lub m₂=√⁵⁵₄ m₁=−^√55₂ lub m₂=^√55₂ m∊(−^√55₂ ,^√55₂ ) −^√55₂< m >^√55₂