rownanie stycznej kartezjusz:

	2
znajdz rownania tej stycznej do wykresu funkcji f(x)=x−		ktora jest prostopadla do
	x2

	−2
prostej okregu okreslonej rownaniem y=		x+1
	3

J:

	3
z warunku: f'(x0) =		wyznacz: x0 ( punkt/ty styczności )
	2

kartezjusz: f'(x₀)=3/2

	4
f'(x)=1−
	x3

wyliczylam pochodne, przyrownalam je do siebie i wyszlo mi x=−2 a=3/2 dobrze? co dalej?

kartezjusz: f'(x₀)=3/2

	4
f'(x)=1−
	x3

wyliczylam pochodne, przyrownalam je do siebie i wyszlo mi x=−2 a=3/2 dobrze? co dalej?

kartezjusz: f'(x₀)=3/2

	4
f'(x)=1−
	x3

wyliczylam pochodne, przyrownalam je do siebie i wyszlo mi x=−2 a=3/2 dobrze? co dalej?

kartezjusz:

J: w pochodnej znak "+" ... i wynik x₀ = 2 ( to jest punky styczności )

	3
teraz styczna: y =		(x − x0) + f(x0)
	2

Janek191:

	2
k : f(x) = −		x + 1
	3

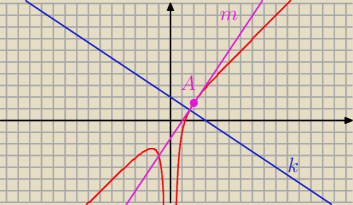
Pochodna źle policzona !

	4		3
f '(x) = 1 +		=
	x3		2

4		1
	=
x3		2

1		1
	=
x3		8

x = 2 =====

	2
f(2) = 2 −		= 1,5
	4

A = ( 2; 1,5) − punkt styczności ==========

	3
y =		x + b i ma przechodzić przez A
	2

1,5 = 1,5*2 + b b = − 1,5 m : f(x) = 1,5 x − 1,5 ==================

kartezjusz: wedlug odp. y=1,5x−2,5

J: y = 1,5x − 1,5 to poprawna odpowiedź