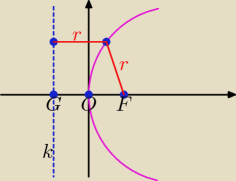
 Krzywa określona równaniem y2 = 2px, to parabola o ognisku w punkcie F i kierownicy k.
Jej wierzchołek leży w punkcie O(0, 0).
p − parametr paraboli, p = |GF|, |GO| = |OF|
Krzywa określona równaniem y2 = 2px, to parabola o ognisku w punkcie F i kierownicy k.
Jej wierzchołek leży w punkcie O(0, 0).
p − parametr paraboli, p = |GF|, |GO| = |OF|

| |y"| | ||
Krzywizna: k = | ||
| (1 + y'2)3/2 |
| 1 | ||
Promień krzywizny: R = | ||
| k |
| 1 | √2*p | |||
y' = √2*p* | *x−1/2 = | |||
| 2 | 2*√x |
| 1 | −1 | −√2*p | ||||
y" = √2*p* | * | *x−3/2 = | ||||
| 2 | 2 | 4*x*√x |
| |||||||||||
k = | |||||||||||
|
| √2*p | √(4*x)3 | |||
k = | * | |||
| 4*x*√x | √(4*x + 2*p)3 |
| 2*√2*p | ||
k = | ||
| √(4*x +2*p)3 |
| 2*√2*p | 1 | |||
k = | = | |||
| 2*p*√2*p | p |
| 1 | ||
R = | = p | |
| k |