Zadanka
Benny: Oblicz prawdopodobieństwo, że przy czterokrotnym rzucie kostka sześcienną trzy kolejne wyniki
utworzą ciąg geometryczny.
|Ω|=6
4
jeśli weźmiemy 1 jako pierwszy wyraz to kolejny może być {1,2,3,4,5,6}
ale, kostka ma cyfry {1,2,3,4,5,6}, więc iloraz może być stały lub równy 2, ponieważ gdy będzie
to cyfra 3, trzeci wyraz byłby równy 9 co jest niemożliwe.
mamy takie możliwości (1,2,4) (4,2,1) (1,1,1) (2,2,2) ... (6,6,6)
dla ciągów (1,2,4) oraz (4,2,1) mamy po 12 możliwości, więc łącznie będzie 24
dla ciągów o ilorazie stałym mamy po 1 możliwości ustawienia "trójki" + 10 innej cyfry (dobrze
myślę?) możliwości, więc |A|=24+6*11=90
18 mar 19:51
Mila:
Wynik dobry, rozumowanie też, zapisy dałabym tak:
A={(k,k,k,m) lub (m,k,k,k) lub (1,2,4,k) lub (k,1,2,4) lub (4,2,1,k) lub (k,4,2,1) gdzie k,
m∊{1,2,3,4,,5,6}}
|A|=6*6+6*6−6+4*6=90
18 mar 20:44
Benny: Możesz powiedzieć czemu tak policzyłaś |A|?

18 mar 20:48
Mila:
Policzyłam tak samo jak Ty, tylko zapisałam inaczej.
(k,k, k, m) zdarzenie: np.(1,1,1,m) i m∊{1,2,3,4,5,6}
Wśród tych zdarzeń będzie (1,1,1,1)
Zdarzeń będzie 36.
(m,k,k,k) , m∊{1,2,3,4,5,6} np(m,1,1,1) Wśród tych zdarzeń będzie (1,1,1,1) zatem dwa razy
policzone (1,1,1,1),(2,2,2,2), ,... to odjęłam 6 zdarzeń. Itd.
Coś się nie zgadza?
18 mar 20:58
Benny: Wszystko ok. Musiałem sobie to poukładać tylko

18 mar 21:01
Mila:
Dla relaksu:
5) Ze zbioru liczb {1,2,3,4,...1993} losujemy jedną liczbę .
Obliczyc prawdopodobieństwo zdarzenia ,że wylosowana liczba jest podzielna pprzez 12 lub 15.
18 mar 21:08
Benny: | | 421 | |
P(A)= |
| ?  |
| | 1993 | |
18 mar 21:23
Benny: Nieee coś mi nie pasuje

18 mar 21:30
Benny: 166 będzie liczb podzielnych przez 12. Zrobiłem to tak obliczyłem ile jest podzielnych przez 3
i przez 4 i odjąłem od siebie, ale z 15 coś tak nie wychodzi
18 mar 21:32
Benny: | | 299 | |
P(A)= |
| ale nie wiem czemu jak robię tak z 15 to muszę podzielić jeszcze przez 2  |
| | 1993 | |
18 mar 21:33
Mila:
|Ω|=1993
A− zdarzenie polegające na tym, że wylosowana liczba jest podzielna przez 12.
| | 1993 | |
|A|=[ |
| ]=166 (albo liczysz z ciągu arytmetycznego ) |
| | 12 | |
B− zdarzenie polegające na tym, że wylosowana liczba jest podzielna przez 15.
A∩B− zdarzenie polegające na tym, że wylosowana liczba jest podzielna prze 12 i przez 15 ,
czyli
NWW(12,15)=60
P(A∪B)=P(A)+P(B)−P(A∩B)⇔
| | 166+132−33 | |
P(A∪B)= |
| =.. |
| | 1993 | |
18 mar 22:07
Benny: Jeju... po co ja zacząłem kombinować z tymi podzielnościami przez 3,4,5
18 mar 22:15
Benny: Może jakieś zadanka na jutro?

18 mar 22:24
Mila:
6) iloczyn pewnych trzech liczb pierwszych równa sie ich pięciokrotnej sumie. Co to za liczby?
7) Rozwiąż nierówność 2x+log(1+4x)≥x log(25)+log(6)
8) Ze zbioru liczb {1,2,3,4,...n} losujemy kolejno ( bez zwracania ) dwie liczby i od pierwszej
odejmujemy drugą.
Obliczyć prawdopodobieństwo p, że różnica jest mniejsza od 2.
18 mar 22:39
Benny: Dziękuje i dobranoc

18 mar 22:42
Mila:
Dobranoc

18 mar 22:45
Benny: W zadanku nr 6) wychodzi parę rozwiązań, ale trzeba niektóre odrzucić ze względu na to, że
muszą być liczbą pierwsza, więc zostają rozwiązania (2,7,5)
| | 1 | |
zadanie nr 7) wychodzi równanie wykładnicze x∊< |
| ;+∞) |
| | 2 | |
no i zadanko nr 8) mam nadzieje, że będzie dobrze
|Ω|=n*(n−1)
A'−różnica jest większa bądź równa 2
| | 1+n−2 | |
i tutaj zrobiłem sumę ciągu Sn= |
| *(n−2) |
| | 2 | |
S
n=|A'|
P(A)=1−P(A')
19 mar 17:18
Mila:
Wszystko zgadza się.

19 mar 17:23
Benny: O proszę

Jakiś inny sposób na to zadanko z prawdopodobieństwem?
19 mar 17:30
Mila:
To bardzo dobry sposób.
19 mar 17:48
Benny: To się bardzo cieszę

19 mar 17:59
Mila:
Widziałam tu zadanie z ostrosłupem dla Ciebie, jak nie znajdę, to napiszę podobne.
19 mar 18:00
Mila:
9) W sześcianie o wierzchołkach A1,A2,A3,...A8 ponumerowano w sposob losowy wszystkie
krawędzie numerami od 1 do 12. Oblicz prawdopodobieństwo, że z jednego wierzchołka wychodzą
krawędzie o numerach 1,2,3.
Czy możliwe jest takie ponumerowanie , aby suma numerów krawędzi wychodzących z każdego
wierzcholka była taka sama? Odpowiedx uzasadnij.
19 mar 18:17
Benny: Omegę z reguły mnożenia? 12*11*10...*1=12!
|Ω|=12!
mamy powiedzmy wierzchołek A
3, wychodzą z niej trzy krawędzie, więc pierwsza liczba na 3
sposoby, druga na 2 i trzecia na 1(3!)
reszta 9*8*7*...*1=9!
mamy tych wierzchołków 8, więc 8 możliwości
Zawsze zapominam jak policzyć omegę, czy to mają być kombinacje czy wariację

Jeśli suma wszystkich będzie równa 78 to nie da się podzielić na 8, żeby wyszła liczba
naturalna
19 mar 19:46
Jacek: Proszę o wyjaśnienie do 7), bo się jakoś zapętliłem przy 4
x+4
2x≥6
8) robiłem bezpośrednio dla różnicy <2
Chcąc otrzymać łączną ilość wariacji spełniających kryterium sumujemy ilość dostępnych wariacji
dla każdej kolejnej liczby:
(n−1)+(n−1)+(n−2)+(n−3)+(n−4)+....+(n−(n−2))+(n−(n−1))
| | n | |
Suma tego ciągu: S=(n−1)*( |
| +1) |
| | 2 | |
W sumie wychodzi ten sam wynik co przy 1−P(≥2)
19 mar 19:47
Benny: podstawiasz niewiadomą t=4
x
no i masz nierówność (t+3)(t−2)≥0
i z tego t≤−3 ⋁t≥2
t≤−3 jest oczywiście sprzeczne, więc rozwiązujesz t≥2
4
x≥2
2
2x≥2
1
19 mar 19:59
Mila:
Benny, dobrze. Nie wiem czy zapisy masz w brudnopisie pełne.
|Ω|− dobrze , 12 "numerów" mozesz ustawić na 12! sposobów (permutacje).
b) sumy :
| 8s | |
| =78 ⇔4s=78 ( podwójnie są liczone krawędzie ) |
| 2 | |
78 nie jest podzielne przez 4.
19 mar 20:46
Benny: Zapisy do którego zadanka?
19 mar 20:49
Mila:
Ogólnie, np. do (6), czy rozpisałes wszystko?
19 mar 20:53
Benny: Wydaję mi się że tak

19 mar 20:53
Mila:
To dobrze.
19 mar 21:03
Mila:
10) Dwie skośne wzgledem siebie krawędzie ostrosłupa trójkątnego maja długość równą b, a
pozostałe krawędzie mają długość równą a. Oblicz objętość tego ostrosłupa.
11) Pole S trójkąta ABC sełnia równość:
S=a2−(b−c)2, gdzie a,b,c są długościami boków trójkata leżącymi odpowiednio naprzeciw kątów:
α,β,γ.
Wyznacz miarę kata α. ( cosα wystarczy)
19 mar 23:12
Benny: Dziś nie miałem kiedy i jak zrobić te zadanka (wiosna itp,

)Jutro
Milu będziesz miała
czas? Bo chciałbym się wziąć mocno do roboty.
Ps. Gdzieś wyczytałem temat o OM, zadanka kiedyś widziałem w szkole. Teraz nie wiem czy to z
ograniczonej wiedzy nie robiłem tych zadań czy moja szkoła po prostu pokazuje to, ale nie
zachęca.
Nie chcę być ograniczony umysłowo, czemu każda szkoła nie zapewnia rozwijania siebie?

20 mar 23:01
20 mar 23:12
Mila:
Nie przesadzaj, oceniam wysoko Twoją wiedzę i inteligencję.
Wszystko przed Tobą otwarte.
Jutro idź na randkę, to poprawisz sobie humor. Ja idę na imprezę, będę późno w domu.
20 mar 23:12
Benny: Problem w tym, że jutro ostatni dzień przygotowań do konkursu

20 mar 23:15
Mila:
Eta Ci pomoże , wykształciła wielu olimpijczyków .
20 mar 23:17
Benny: Nie zaliczam się do olimpijczyków. Dajmy na to przykład z ostatniej próbnej matury. Ponad
połowa klasy rozwiązała zadanko z planimetrii( trzeba było wykazać równość pól), którego ja
nie rozwiązałem. Pustka, nie widziałem nic.
20 mar 23:20
Mila:
To popracujemy nad planimetria.
A ile % miałeś z próbnej?
20 mar 23:22
Benny: Było parę ich, ale wolę się nie ośmieszać. Nie wiem czemu te zadanka z podstawy czasem wydają
mi się trudniejsze od rozszerzenia. No, ale średnio to 90%+

Zawsze odejmują mi pkt za jakieś braki odp czy coś podobnego

20 mar 23:26
Mila:
To przecież bardzo dobrze, a straty zawsze jakieś są, do matury doszlifujesz wszystko, a potem
popracujesz ,aby nie mieć kłoptów na studiach.
20 mar 23:30
Benny: Milu, Ty może nauczycielką jesteś? Wiem, że głupie pytanie, ale lubię wiedzieć z kim mam
do czynienia

20 mar 23:33
Mila:
Musisz sam wyciągnąć wnioski na podstawie mojej pracy tutaj.
20 mar 23:35
Benny: To nie jest takie proste

Na pierwszy rzut oka mogłabyś powiedzieć, że jestem uczniem klasy
maturalnej?

20 mar 23:39
Mila:
A nie jesteś?
20 mar 23:40
Benny: No oczywiście, że jestem

ale chodziło mi o to, że człowieka nie zawsze możemy rozpoznać
przez pryzmat tego co robi

20 mar 23:42
Patryk: Mila, że się tak wtrącę... Miałabyś jakiś pomysł na powtórkę wszystkiego do matury
rozszerzonej? Uczę już się od jakiegoś czasu i doszlifowywuję się korzystając z poprzednich
arkuszy, ale one są mocno ograniczone (zdaję jeszcze starą maturę − jestem w technikum). Nie
wiem skąd brać jakieś zadania typowo maturalne, a zostało niewiele czasu, właściwie to akurat
własnie na powtórkę

20 mar 23:55
Mila:
Patryk, Arkusze Pazdro z ubiegłych lat były w Necie.
NA Info masz próbne matury dla technikum, więc możesz rozwiązywać.
Może jutro późnym wieczorem coś znajdę, to dam Linki.
21 mar 00:01
21 mar 00:02
21 mar 00:04
Mila:
Dobranoc wszystkim.

21 mar 00:06
Patryk: Dzięki wielkie! Jutro przejrzę, a tymczasem uciekam spać. Jakby Panie znały jeszcze jakieś
strony ciekawe, to proszę się nie krępować z wysłaniem ich

Dobrej nocy życzę!

21 mar 00:06
Benny: Oblicz, ile jest punktów (x,y ) na płaszczyźnie, których współrzędne x i y są liczbami
całkowitymi spełniającymi odpowiednio nierówności: |17 9− x | < 43 i |y+ 372| < 21 .
Wychodzi mi pewna ograniczona figura i nie rozumiem za bardzo jak mam "policzyć" te punkty.
21 mar 09:52
Benny: Ktoś zaglądnie?

21 mar 18:40
Benny: Eta, masz troszkę czasu, żeby pomóc?
21 mar 19:29
Eta:
1/ |x−179|<43 ⇒ x∊(136,222) w tym przedziale mamy
222−136 +1 = 87 liczb całkowitych
2/ |y+372|<21 ⇒ y∊(−393, −351) w tym przedziale mamy:
−351+393+1= 43 liczb całkowitych
Liczymy punkty "kratowe" wewnątrz takiego prostokąta( bez punktów na brzegach
bo przedziały są otwarte
mamy zatem : 87*43− [87*2+(43−2)*2]= .... takich punktów
21 mar 19:59
Benny: Jeśli dobrze myślę to 43−2 jest z racji tego, że nie liczymy dwa razy tych samych punktów?

21 mar 20:03
Eta:
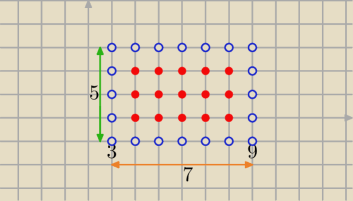
Taki przykład:
1/ x∊(3,9) w nim 7 liczb całkowitych
2/ y∊(2,6) w nim 5 liczb całkowitych
to: 7*5−[2*7+(5−2)*2]= 35 −20=
15 takich
"kropek" par (x, y) ∊C
jasne ?

21 mar 20:08
Benny: Tak, chciałem się tylko upewnić

Wykaż, że dla dowolnej liczby rzeczywistej x spełniona jest nierówność
| | 1 | | 1 | |
( |
| )x4 + ( |
| )x3 > 3x2 − 16. |
| | 4 | | 3 | |
tutaj myślałem coś o pochodnych aby przedstawić za pomocą dwóch funkcji i wykazać za pomocą
monotoniczności
21 mar 20:16
miron: Weź wszystko na jedną stronę. Policz granice w niesk i min. niesk oraz pochodne, extrema i
wykaż ze funkcja jest zawsze >0
21 mar 20:31
jankokoko: Skoro robicie arkusze z zadania.info to poweidźcie mi co z robić w nim
W ostrosłupie prawidłowym trójkątnym krawędć podstawy ma długość a. Kąt między krawędzią boczną
a krawędzią podstawy ma miarę α>30 stopni oblicz obj ostrosłupa
Policzyłem objętość że wynosi
( a3 * √3tg2α −1 ) / 24
Co teraz ? Co mam zrobić z tym faktem że α>30 stopni ?
21 mar 20:34
jankokoko: dobra nie ważne juz wiem
21 mar 20:52
Benny: Oblicz prawdopodobieństwo warunkowe, że w czterokrotnym rzucie symetryczną sześcienną kostką do
gry otrzymamy co najmniej dwie „dwójki”, pod warunkiem że otrzymamy co najmniej jedną
„piątkę”.
21 mar 21:08
Mila:
Ponieważ to jest zadanie z INFO, gdzie trzeba płacić, to aby nie wchodzic w konflikt interesów,
dam wskazówkę.
A− otrzymamy co najmniej jedną piątkę − to łatwo obliczysz.
B− otrzymamy co najmniej dwie „dwójki”, pod warunkiem że otrzymamy co najmniej jedną
„piątkę”.
A∩B
Masz takie zdarzenia sprzyjające :
(5,2,2,X) gdzie x∊{1,3,4,6} , pamiętaj o permutacji
(5,2,2,2) − liczba zdarzeń 4
(5,5,2,2)− liczba zdarzeń ?
21 mar 22:01
Benny: (5,2,2,2)−4
|A∩B|=58
| | 58 | | 1296 | |
P(B|A)= |
| * |
| |
| | 1296 | | 671 | |
| | 58 | |
P(B|A)= |
| ?  |
| | 671 | |
22 mar 18:51
Mila:
Jak tam konkurs?
22 mar 18:52
Benny: Tak jak się spodziewałem, prawdopodobieństwo, którego nie lubię i to jeszcze takie... ze zbioru
{1,2,3...,n} losujemy bez zwracania k liczb i otrzymujemy ciąg a
1,a
2,...,a
k
3≤k≤n
a)jakie jest prawdopodobieństwo, że a
k jest największa
b)jakie jest prawdopodobieństwo, że a
k jest podzielna przez 3
jakoś tak to szło, podpunktu c nie pamiętam
Było też takie: na kuli opisano stożek, promień kuli R=2cm, oblicz wysokość stożka dla którego
objętość jest najmniejsza. Nie wiem co się stało, ale błądziłem w niewiadomych, nie mogłem
uzależnić promienia stożka od wysokości na dodatek cały dzień boli mnie głowa

22 mar 19:01
Mila:

Zobaczymy, jakie nastroje mieli przyszli studenci po wyjściu z sali?
22 mar 19:04
Benny: Śmiać i płakać mi się chciało. Płakać z mojej głupoty, a śmiać z głupoty kumpli z klasy

Jeden zrobił zadanko całkiem odwrotnie, wpisał stożek w kule, drugi jakieś nowe wzory do
trójkąta wymyślił

Co myślisz o tym zadanku z prawdopodobieństwa? Tego co zrobiłem i wstawiłem do zrobienia.
22 mar 19:08
Mila:
Myślę, że obydwa są trudne dla licealisty.
Jakie zadania ( jakiego typu) rozwiązałeś wg Ciebie dobrze?
22 mar 19:45
Benny: Nierówność wymierna, równanie trygonometryczne, coś chyba z analitycznej, 32016+4 jakie ma
dzielniki naturalne mniejsze od 7
coś kombinowałem jeszcze z jakimś równaniem |mx2−2x|=m ale nie mogłem za bardzo zrozumieć
treści. Coś tam było, że suma pierwiastków tego równania przyporządkowuje wartość m? Jakoś
tak, trzeba było narysować do tego wykres g(m)
22 mar 19:52
Benny: Nierówność wykładnicza*

Możemy te zadanka spróbować rozwiązać?
22 mar 20:11
Mila:
To nie jest tak źle.
22 mar 20:22
Mila:
Może dzisiaj odpocznij, ale oczywiście możemy.
22 mar 20:23
Benny: To pewnie jutro się będę odzywał, a teraz najwyżej sobie jakieś maturki z podstawy porobię

22 mar 20:32
Benny:
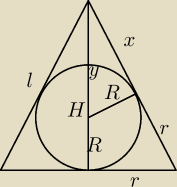
R=2cm
H=y+R y=H−R
l=x+r x=l−r
| ⎧ | H2+r2=l2 | |
| ⎩ | (H−R)2=R2+(l−r)2 |
|
H
2−4H+4=4+l
2−2lr +r
2
tutaj za l
2 wstawiłem H
2+r
2
H
2−4H=H
2+r
2−2
√H2+r2*r +r
2
−4H=2r
2−2
√H2+r2*r
√H2+r2*r=r
2+2H /:r
| | 2H | | 4H2 | |
H2+r2=r2+2*r* |
| + |
| |
| | r | | r2 | |
H
2*r
2=4H*r
2+4H
2
r
2*(H
2−4H)=4H
2
| | 1 | | 8H*(H−4)−4H2 | |
V'(H)= |
| *π* |
| |
| | 3 | | (H−4)2 | |
punkty krytyczne, więc przyrównujemy licznik do 0
4H
2−32H=0
4H*(H−8)=0
dla H=8 jest minimum, więc dla H=8 objętość jest najmniejsza
Jaki ja jestem głupi... robiłem tak cały czas, ale gdy dochodziłem do pierwiastka
√H2+r2 to
się poplątałem i myślałem, że cały czas coś źle robię. Czemu zawsze po fakcie wszystko wraca
do głowy

23 mar 17:50
Mila:
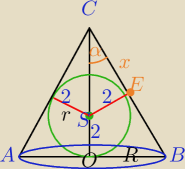
Może tak trochę mniej liczenia:
|OC|=h, h>0
r=2− promień okręgu wpisanego w ΔABC
W ΔCOB:
W ΔCES:
x
2+2
2=(h−2)
2
x
2+4=h
2−4h+4
x
2=h
2−4h podstawiając do (2)
| | 4π | | 2h*(h−4)−h2 | |
V'(h)= |
| * |
| |
| | 3 | | (h−4)2 | |
V'(h)=0⇔h=8
V'(h)>0⇔h<0 lub h>8
dla h=8 V(h) ma min
V(8)=...
23 mar 18:31
Benny: Mój pierwszy pomysł był taki, żeby może jakoś z trygonometrii policzyć, ale pomyślałem, że z
układu będzie pewniej

23 mar 19:06
Benny: Mój pierwszy pomysł był taki, żeby może jakoś z trygonometrii policzyć, ale pomyślałem, że z
układu będzie pewniej

23 mar 19:06
Mila:
W obu sposobach jest trochę liczenia.
23 mar 20:50
Benny: Myślałaś coś może nad tym prawdopodobieństwem?
23 mar 21:07
Mila:
Oj, nie, boli głowa od samego czytania, jak odpocznę to przeczytam i pomyślę.
Wolę coś mniej abstrakcyjnego. Przecież nie ma pośpiechu.
23 mar 21:09
Benny: Jasne, że nie

To może jakieś normalne zadanka są do zrobienia?
23 mar 21:25
Mila:
Widzę, że z okręgiem wpisanym w Δ coś trzeba robic. Miałam Ci podrzucić przed konkursem, ale
jakoś umknęło ( a szkoda) .
1)
| | 1 | |
W wycinek koła o promieniu R wpisany jest okrąg o promieniu |
| R. |
| | 3 | |
Oblicz pole wycinka koła.
23 mar 22:04
Benny:
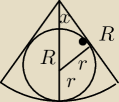
x=30
o
2x=60
0
24 mar 16:31
Mila:
+
24 mar 16:52
Benny: Nie no ja chyba trochę ogarniam te okręgi wpisane, ale na konkursie chyba stres mnie zjadł

24 mar 16:54
Mila:
Benny to było trudne zadanie, kiedy wyniki?
24 mar 17:08
Mila:
2) wyznacz zbiór wartości funkcji:
f(x)=2cosx−cos(2x) dla x∊<0,2π>
24 mar 17:15
Benny: Nie mam pojęcia kiedy wyniki, ale wiem i tak, że nie mam na co liczyć.
24 mar 17:32
5-latek : Ale za to masz jakie doswiadczenie przed egzaminen maturalnym

Inni tego nie maja . Ty juz masz
24 mar 17:38
Benny: | | 1 | |
Zwf ∊<−3;1,5>, p= |
| ∊<−1;1> |
| | 2 | |
24 mar 17:41
Mila:
+

25 mar 15:52
Benny: a powiedz mi czy dobrze to robiłem, bo doprowadziłem to do postaci −2cos
2x+2cosx+1
cosx=t
−2t
2+2t+1=0
| | 1 | |
i tutaj liczę f(1), f(−1) i f( |
| ) ? |
| | 2 | |
25 mar 16:08
Mila:
Dobrze.
zał. po podstawieniu: t∊<−1,1>
| | 1 | | 1 | |
xw= |
| ∊<−1,1>⇔dla x= |
| funkcja f(t) ma wartość największą w tym przedziale. |
| | 2 | | 2 | |
Najmniesza wartość na końcu przedziału, wybierasz.
25 mar 17:52
Mila:
Jeszcze trzeba zbadać, czy te wartości są przyjmowane w przedziale <0,2π>.
25 mar 18:16
Benny:
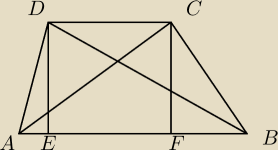
Założenie miałem, ale tu nie dopisałem. Mam teraz mały problem z dowodem

Czworokąt ABCD jest trapezem o podstawach AB i CD. Wykaż że
|AC|
2 + |BD|
2 = |AD|
2 + |BC|
2 + 2|AB|⋅|DC|.
Próbowałem pitagorasa do ADE, BCF, ACF, BDE, ale chyba nie tędy droga, bo dziwne równania
powychodzą jak wszystko wymnożę
25 mar 18:18
Benny: Robiłem dwa razy na cosinusach, za pierwszym razem tak to sobie wymnożyłem, że nie wiedziałem
już co do czego i myślałem, że źle.
Blue napisała, że na cosinusach robiła, więc
spróbowałem jeszcze raz i pykło

25 mar 21:14
Mila:

25 mar 21:27
Mila:
Załóż nowy wątek z problemowym zadaniem.
25 mar 21:28









 Jakiś inny sposób na to zadanko z prawdopodobieństwem?
Jakiś inny sposób na to zadanko z prawdopodobieństwem?

 Jeśli suma wszystkich będzie równa 78 to nie da się podzielić na 8, żeby wyszła liczba
naturalna
Jeśli suma wszystkich będzie równa 78 to nie da się podzielić na 8, żeby wyszła liczba
naturalna

 )Jutro Milu będziesz miała
czas? Bo chciałbym się wziąć mocno do roboty.
Ps. Gdzieś wyczytałem temat o OM, zadanka kiedyś widziałem w szkole. Teraz nie wiem czy to z
ograniczonej wiedzy nie robiłem tych zadań czy moja szkoła po prostu pokazuje to, ale nie
zachęca.
Nie chcę być ograniczony umysłowo, czemu każda szkoła nie zapewnia rozwijania siebie?
)Jutro Milu będziesz miała
czas? Bo chciałbym się wziąć mocno do roboty.
Ps. Gdzieś wyczytałem temat o OM, zadanka kiedyś widziałem w szkole. Teraz nie wiem czy to z
ograniczonej wiedzy nie robiłem tych zadań czy moja szkoła po prostu pokazuje to, ale nie
zachęca.
Nie chcę być ograniczony umysłowo, czemu każda szkoła nie zapewnia rozwijania siebie?
 http://www.wolframalpha.com/input/?i=%E2%88%92x3%2B6x2%E2%88%9211x%2B6%3E0
http://www.wolframalpha.com/input/?i=%E2%88%92x3%2B6x2%E2%88%9211x%2B6%3E0

 Zawsze odejmują mi pkt za jakieś braki odp czy coś podobnego
Zawsze odejmują mi pkt za jakieś braki odp czy coś podobnego 

 Na pierwszy rzut oka mogłabyś powiedzieć, że jestem uczniem klasy
maturalnej?
Na pierwszy rzut oka mogłabyś powiedzieć, że jestem uczniem klasy
maturalnej? 
 ale chodziło mi o to, że człowieka nie zawsze możemy rozpoznać
przez pryzmat tego co robi
ale chodziło mi o to, że człowieka nie zawsze możemy rozpoznać
przez pryzmat tego co robi 


 Dobrej nocy życzę!
Dobrej nocy życzę! 


 Taki przykład:
1/ x∊(3,9) w nim 7 liczb całkowitych
2/ y∊(2,6) w nim 5 liczb całkowitych
to: 7*5−[2*7+(5−2)*2]= 35 −20= 15 takich "kropek" par (x, y) ∊C
jasne ?
Taki przykład:
1/ x∊(3,9) w nim 7 liczb całkowitych
2/ y∊(2,6) w nim 5 liczb całkowitych
to: 7*5−[2*7+(5−2)*2]= 35 −20= 15 takich "kropek" par (x, y) ∊C
jasne ? 
 Wykaż, że dla dowolnej liczby rzeczywistej x spełniona jest nierówność
Wykaż, że dla dowolnej liczby rzeczywistej x spełniona jest nierówność


 Zobaczymy, jakie nastroje mieli przyszli studenci po wyjściu z sali?
Zobaczymy, jakie nastroje mieli przyszli studenci po wyjściu z sali?
 Jeden zrobił zadanko całkiem odwrotnie, wpisał stożek w kule, drugi jakieś nowe wzory do
trójkąta wymyślił
Jeden zrobił zadanko całkiem odwrotnie, wpisał stożek w kule, drugi jakieś nowe wzory do
trójkąta wymyślił  Co myślisz o tym zadanku z prawdopodobieństwa? Tego co zrobiłem i wstawiłem do zrobienia.
Co myślisz o tym zadanku z prawdopodobieństwa? Tego co zrobiłem i wstawiłem do zrobienia.
 Możemy te zadanka spróbować rozwiązać?
Możemy te zadanka spróbować rozwiązać?

 R=2cm
H=y+R y=H−R
l=x+r x=l−r
R=2cm
H=y+R y=H−R
l=x+r x=l−r

 Może tak trochę mniej liczenia:
|OC|=h, h>0
r=2− promień okręgu wpisanego w ΔABC
W ΔCOB:
Może tak trochę mniej liczenia:
|OC|=h, h>0
r=2− promień okręgu wpisanego w ΔABC
W ΔCOB:


 To może jakieś normalne zadanka są do zrobienia?
To może jakieś normalne zadanka są do zrobienia?


 Inni tego nie maja . Ty juz masz
Inni tego nie maja . Ty juz masz

 Założenie miałem, ale tu nie dopisałem. Mam teraz mały problem z dowodem
Założenie miałem, ale tu nie dopisałem. Mam teraz mały problem z dowodem  Czworokąt ABCD jest trapezem o podstawach AB i CD. Wykaż że
|AC|2 + |BD|2 = |AD|2 + |BC|2 + 2|AB|⋅|DC|.
Próbowałem pitagorasa do ADE, BCF, ACF, BDE, ale chyba nie tędy droga, bo dziwne równania
powychodzą jak wszystko wymnożę
Czworokąt ABCD jest trapezem o podstawach AB i CD. Wykaż że
|AC|2 + |BD|2 = |AD|2 + |BC|2 + 2|AB|⋅|DC|.
Próbowałem pitagorasa do ADE, BCF, ACF, BDE, ale chyba nie tędy droga, bo dziwne równania
powychodzą jak wszystko wymnożę

