Udowodnij, że jeżeli liczby rzeczywiste a i b spełniają równość a+b=1, to: Dżeki: Udowodnij, że jeżeli liczby rzeczywiste a i b spełniają równość a+b=1, to: a²+b²≥1/2 a³+b³≥1/4 a⁴+b⁴≥1/8

Dżeki: ok.. wiem, że w podpunkcie a wystarczy skorzystać z zależności a²+b²/2≥(a+b)²/2 Ma ktoś pomysł na b i c ?

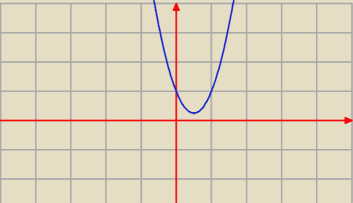
Janek191: a + b = 1 ⇒ b = 1 − a więc a³ + b³ = a³ + ( 1 − a)³ = a³ + 1 − 3 a + 3 a² − a³ = 3 a² − 3 a + 1 Mamy funkcję kwadratową f(a) = 3 a² − 3 a + 1 Szukamy jej najmniejszej wartości

	3
p =		= 0,5
	6

więc

	1
q = f( 0,5) = 3*0,25 − 3*0,5 + 1 = 0,75 − 1,5 + 1 = 0,25 =
	4

więc

	1
a3 + b3 ≥
	4

=============== ckd.

Dżeki: c już też gotowe, więc dziękuję !

Eta: Z nierówności między średnimi potęgową i arytmetyczną

	a3+b3		a+b		1
3√		≥		=		/3
	2		2		2

	a3+b3		1
		≥		/*2
	2		8

	1
a3+b3≥
	4

podobnie:

	a4+b4		a+b
4√		≥
	2		2

..................... c.n.u