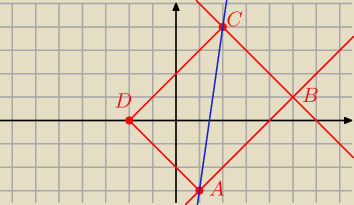
geometria analityczna lawenderr: W prostokacie ABCD dane sa: wierzcholek C(2;4) i wektor AB=[4;4]. Wyznacz rownanie ogolne prostej zawierajacej przekatna AC tego prostokata, jesli wiadomo, ze wierzcholek A nalezy do prostej k: x−y−4=0 Wiec kierujac sie wskazowkami w odpowiedziach, wyznaczylam rownanie ogolne prostej zawierajacej bok BC (prostopadla do wektora). Nie wiem jak dalej obliczyc wspolrzedne A i B. Probowalam podstawiac do rownan prostych do ktorych te punkty naleza o do wektora AB ale nie wychodzi.

Janek191: k : x − y − 4 = 0 ⇒ y = x − 4 Prosta prostopadła do k przechodząca przez C : y = − x + b C = ( 2 , 4) 4 = − 2 + b b = 6 l : y = − x + 6 −−−−−−−−−−−−−−−−− y = x − 4 y = − x + 6 więc x − 4 = − x + 6 2 x = 10 x = 5 y = 1 B = ( 5 , 1) ========= A = ( 5 − 4, 1 − 4) = ( 1, − 3) ====================== D = ( 2 − 4, 4 − 4) = ( − 2 , 0) ====================== Mamy A = ( 1 , − 3) i C = ( 2, 4) Prosta AC

	y2 − y1
y − y1 =		*( x − x1)
	x2 − x1

	4 − (−3)
y − ( − 3) =		*( x − 1)
	2 − 1

y + 3 = 7*( x − 1) y = 7 x − 7 − 3 y = 7 x − 10 ========== lub 7 x − y − 10 = 0 ==============