18 mar 17:18
Janek191:
α = I ∡ CPA I
i PA I = x
I P B I = x + 10
Z tw. o siecznej mamy
x*( x + 10) = 12
2
x
2 + 10 x − 144 = 0
Δ = 100 − 4*1*( − 144) = 100 + 576 = 676
√Δ = 26
więc
I P A I = 8 i I PB I = 18
oraz
| I PC I | | I PB I | |
| = |
| |
| I PA I | | I P CI | |
bo
zatem
boki leżące przy kącie α są proporcjonalne w skali k = 1,5
I PC I = 1,5 * I PA I
oraz
I PB I = 1,5 I P C I
więc trójkąty : Δ PCA , Δ PCB są podobne.
=====================================
18 mar 20:26
Blue: Aha, czyli Ty udowadniasz podobieństwo na podstawie tw. o siecznej, bo ja chciałam na podstawie
twierdzenia o kącie dopisanym...
A to 1 jak zrobić?

18 mar 22:40
Blue: Dzięki za odp. Janek

18 mar 22:45
Qulka:
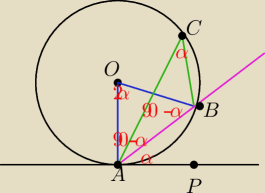
kąt OAB = 90−α bo styczna jest ⊥ do promienia
kąt OBA = kąt OAB bo równoramienny ( ramiona to promień)
więc kąt AOB = 2α bo suma =180°
kąt ACB =α bo wpisany o połowę mniejszy niż środowy
18 mar 23:39
Blue: Dziękuję !

18 mar 23:50
Eta:
|<PAB| −− kąt dopisany =|<ACB|−−− kąt wpisany oparty na łuku AB
19 mar 00:16
Qulka: Etuś i to ma być dowód

19 mar 00:22

 http://i60.tinypic.com/o6ivko.jpg
I czy to twierdzenie z tego dowodu można po prostu wykorzystać w zadaniu 76? Czy jeszcze
trzeba to twierdzenie udowadniać? Jak to jest?
http://i60.tinypic.com/o6ivko.jpg
I czy to twierdzenie z tego dowodu można po prostu wykorzystać w zadaniu 76? Czy jeszcze
trzeba to twierdzenie udowadniać? Jak to jest? http://i57.tinypic.com/sazmrq.jpg
http://i57.tinypic.com/sazmrq.jpg


 kąt OAB = 90−α bo styczna jest ⊥ do promienia
kąt OBA = kąt OAB bo równoramienny ( ramiona to promień)
więc kąt AOB = 2α bo suma =180°
kąt ACB =α bo wpisany o połowę mniejszy niż środowy
kąt OAB = 90−α bo styczna jest ⊥ do promienia
kąt OBA = kąt OAB bo równoramienny ( ramiona to promień)
więc kąt AOB = 2α bo suma =180°
kąt ACB =α bo wpisany o połowę mniejszy niż środowy

