uzasadnij pochodna:

	x−4
uzasadnij ze styczne do wykresu funkcji f(x)=		w punktach przeciecia tego wykresu z
	x−2

osiami ukladu wspolrzednych sa rownolegle

J: 1) znajdź punkty przecięcia 2) pokaż,że f'(x_i) ma tą samą warość ( x_i odcieta punktu przecięcia)

Janek191: x ≠ 2

x − 4
	= 0 ⇔ x = 4
x − 2

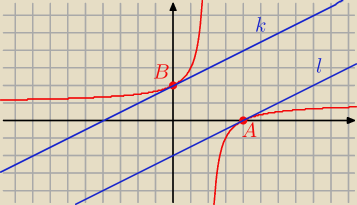
A = ( 4, 0) =========

0 − 4
	= 2
0 − 2

B = ( 0, 2) ========= oraz

	x − 2 − ( x − 4)		2
f '( x) =		=
	( x − 2)2		( x − 2)2

więc

	2		2
a 1 = f ' ( 0) =		= 0,5 oraz a2 = f '(4) =		= 0,5
	4		4

a₁ = a₂ zatem proste styczne są równoległe ======================================== y = 0,5 x + b 2 = b k : y = 0,5 x + 2 ============== y = 0,5 x + b₁ 0 = 0,5*4 + b₁ b₁ = − 2 l : y = 0,5 x − 2 ==============

J: wyznaczenie stycznych , to już nadgorliwość

Janek191: Ładniejszy rysunek