2 Foxal: zadanie 2 W trojkacie prostokatnym ABC, gdzie I∠CABI=90^o, poprowadzono srodkowa AD, ktorej dlugosc jest rowna 5 cm. Wiedzac, ze dlugosci bokow trojkata tworza ciag arytmetyczny, oblicz sinI∠ADCI BC=2AD=10 i AB=a {a=a1 lub a=a1+r} oraz AC=b {b=a1 lub b=a1+r} a1+2r=10 10²=a²+b² 100=a²1+(a1+r)² 2a¹+2a1r+r²=100 2a1(a1+2r)+r²=100 20a1+r²=100 20(10−2r)+r²=100 (a1=10−2r) r²−40r+100=0 i nie wychodzi mi

J: boki: x − r , x , 10 2x = x − r ⇔ x = 10 − r (x − r)² + x² = 100 ⇔ (10 −2r)² + (10 − r)² =100 ⇔ r = 10 lub r = 2 ( r =10 odpada )

J: ostatecznie boki trójkąta: 6 , 8 , 10

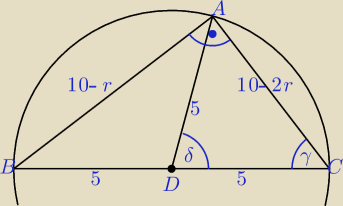
Bogdan: 10 − 2r > 0 ⇒ r < 5 (10 − r)² + (10 − 2r)² = 10² ⇒ r = 2 < 5 lub r = 10 > 5

	10 − 2
sinγ =		,
	10

sinδ można wyznaczyć korzystając z twierdzenia sinusów w trójkącie ADC:

10 − 2r		5
	=		⇒ sinδ = ...
sinδ		sinγ

Foxal: dzieki