1 Foxal: Zadanie 1 W trojkacie prostakatnym ABC przeciwprostokatna BC ma dlugosc 13. Stosunek promienia kola wpisanego w ten trojkat do promienia kola opisanego na tym trojkacie wynosi 4/13. Oblicz tangensy katow ostrych tego trojkata. Więc: R=BC/2=13/2 4/13=r/(13/2) 52=26r r=2 I∠ABCI=α i I∠ACBI=β oraz srodkowa poprowadzona na przyprostokatna tworzy odcienek AD I∠ADBI=γ i I∠ADCI=δ IADI=ICBI więc I∠BADI=I∠ABDI=α analogicznie I∠DACI=IACBI=β po rozwiazaniu ukladu rownan z {2α+γ=180^o i 2β+δ=180^o} oraz γ+δ=180^o wychodzi ze α=β=45^o i IABI=IACI sinα=IABI/13 IABI=(13√2)/2 prosze o wskazowke jak to dalej zrobic

J: jak na razie , z Twojego układu równań wychodzi,że: α + β = 90 ( co jest oczywiste )

Foxal: γ=δ=90 nawet jakbym nie znal wlasnosci to bym udowonil ze γ=90 2α+γ=180^o i γ+δ=180^o 2α+γ=γ+δ 2α=δ⇔2β=γ czyli skoro α jest katem przy podstawie i trojkata rownoramiannego to z rownosci wynika ze kat miedzy ramionami jest dwa razy wiekszy od kata α czyli α=45^o, takze 2*45^o+δ=180 ⇒ δ=90^o ale mniejsza z tym bo pewnie w pierwszym poscie cos zle oznaczylem albo zle spojrzales. Jak obliczyc te tangensy?

J: nieźle namieszałeś ... co to jest u Ciebie odcinek AD ?

Foxal: srodkowa poprowadzona z kata prostego

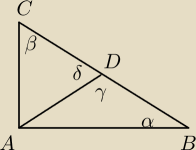
J: i teraz wykaż jakim cudem : γ = δ = 90⁰ ...?