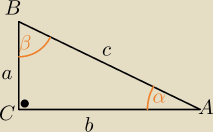Trygonometria: trójkąt prostokątny, oblicz wartość wyrażenia.
:): W trójkącie prostokątnym o kątach ostrych α i β dane jest wyrażenie: √tg2α + 1*sinβ
Oblicz wartość tego wyrażenia.
Jak zacząć to zadanie?
Z góry dziękuję za pomoc!
17 mar 21:02
Eta:
dla kąta ostrego sinβ= cosα
| | sin2α | | sin2α+cos2α | | 1 | |
tg2α= |
| to tg2α+1= |
| = |
| |
| | cos2α | | cos2α | | cos2α | |
| | 1 | | 1 | |
to W= |
| *sinβ= |
| *cosα= 1 |
| | cosα | | cosα | |
17 mar 21:52
Mila:
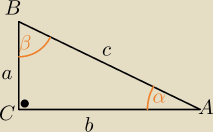
============
√tg2α+1* sinβ
| | sin2α+cos2α | |
=( |
| })12*sinβ= |
| | cos2α | |
| | 1 | | 1 | |
= |
| *sinβ= |
| *cosα=1 |
| | cosα | | cosα | |
17 mar 21:55
Eta:

17 mar 21:56
:): Czyli jednak ten wzór z tangensem... Dziękuję Wam bardzo!

17 mar 23:32