trapez Blue: Długości podstaw trapezu są równe 6 i 9, a ramiona mają długości 2 i 4. Oblicz cosinusy kątów tego trapezu. Może jakaś podpowiedź

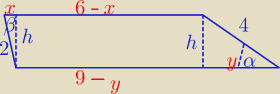
Janek191: Może jest tak ?

jakubs: Zacznij od wyznaczenia przekątnych i oczywiście od dobrego rysunku.

Janek191: 6 − x = 9 − y y − x = 3 y = x + 3 więc h² + ( x + 3)² = 16 h² + x² = 4 −−−−−−−−− x² + 6 x + 9 − x² = 12 6 x = 3 x = 0,5 y = 3,5

	y		7
cos α =		=
	4		8

	x		1
cos β =		=
	2		4

Janek191: 6 − x = 9 − y y − x = 3 y = x + 3 więc h² + ( x + 3)² = 16 h² + x² = 4 −−−−−−−−− x² + 6 x + 9 − x² = 12 6 x = 3 x = 0,5 y = 3,5

	y		7
cos α =		=
	4		8

	x		1
cos β =		=
	2		4

Blue: Ale dziwny ten trapez To już wyjaśnia, dlaczego x mi wychodziło ujemne ... Dzięki wielkie!

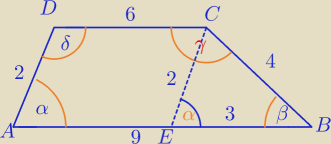
Mila: CE||AD α+δ=180 β+γ=180 W ΔCEB: z tw. cosinusów: 2²=3²+4²−2*3*4 cosβ

	21
cosβ=
	24

	21
cosγ=−
	24

W ΔCEB: z tw. cosinusów: 4²=2²+3²−2*2*3 cosα

	−1
cos α=		z tego wniosek, że α− kat rozwarty i rysunek ma wyglądać tak jak u Janka
	4

	1
cosδ=		i α− kąt ostry.
	4

Janek191: cd.

	7
cos γ = ( 180o − α ) = − cos α = −
	8

	1
cos δ = cos ( 180o − β) = − cos β = −
	4

jakubs: Mila świetny pomysł

Blue: Mila dzięki również Tobie, Janek nie musiałeś, już sobie poradziłam