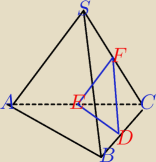
 Ostrosłup prawidłowy trójkątny o krawędzi podstawy a przecięto płaszczyzną przechodzącą przez
środki krawędzi wychodzących z wierzchołka C. Pole otrzymanego przekroju jest równe S. Wyznacz
objętość tego ostrosłupa.
Ostrosłup prawidłowy trójkątny o krawędzi podstawy a przecięto płaszczyzną przechodzącą przez
środki krawędzi wychodzących z wierzchołka C. Pole otrzymanego przekroju jest równe S. Wyznacz
objętość tego ostrosłupa.
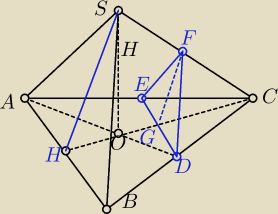 AB = BC = CA = a
DE || AB
AB = BC = CA = a
DE || AB
| AB | a | |||
DE = | = | |||
| 2 | 2 |
| DE*GF | |
= S | |
| 2 |
| 4S | ||
GF = | ||
| a |
| 8S | ||
HS = 2GF = | ||
| a |
| a√3 | ||
HC = | ||
| 2 |
| 1 | a√3 | |||
OH = | HC = | |||
| 3 | 6 |
| a2√3 | H | |||
V = | * | = | ||
| 4 | 3 |