| x2−x−6 | ||
Do zbioru rozwiązań nierówności | ≤0 należy każda liczba z liczb: | |
| 8−x |
 ( x2 − x − 6)*( 8 − x) ≤ 0
( x − 3)*( x + 2)*( 8 − x) ≤ 0
x1 = − 2 x2 = 3 x3 = 8 − miejsca zerowe
f( 10) = 7*12*( − 2) < 0
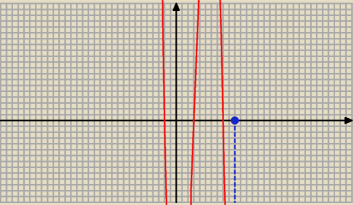
więc szkicujemy wykres funkcji i odczytujemy rozwiązanie
x ∊ < − 2, 3> ∪ < 8 , + ∞)
Do tego zbioru należą liczby: 0,1 , 3 ,11, 13
( x2 − x − 6)*( 8 − x) ≤ 0
( x − 3)*( x + 2)*( 8 − x) ≤ 0
x1 = − 2 x2 = 3 x3 = 8 − miejsca zerowe
f( 10) = 7*12*( − 2) < 0
więc szkicujemy wykres funkcji i odczytujemy rozwiązanie
x ∊ < − 2, 3> ∪ < 8 , + ∞)
Do tego zbioru należą liczby: 0,1 , 3 ,11, 13