Oblicz promień mniejszego z dwóch okręgów stycznych Kasia: Oblicz promień mniejszego z dwóch okręgów stycznych w punkcie M(2, 1) do prostej x−7y +5 = 0 i jednocześnie stycznych do prostej x+y +13 = 0. Obliczyłam to wyznaczając równanie tego okręgu, ktoś może widzi prostszy sposób? Czasem działają np. "tricki" z podobieństwem trójkątów.

akka: Gdzie te okręgi? jakie? bo nie widzę?

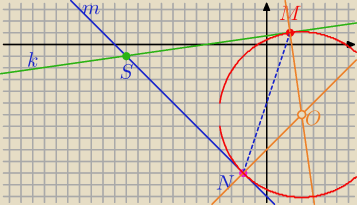
Mila: Środek okręgu stycznego do ramion kąta leży na dwusiecznej tego kąta

	1		5
k: y=		x+
	7		7

m: y=−x−13 S=(−12,−1) SM^→=[14,2] |SM|=√14²+2²=√200=10√2 Układ: (x+12)²+(y+1)²=200 y=−x−13 i x>−12 ⇔ N=(−22,9) nie odpowiada lub N=(−2,−11) Punkt przecięcia prostopadłej do k w punkcie M i prostopadłej do m w punkcie N jest środkiem szukanego okręgu. y=−7x+15 y=x−9 O=(3,−6) r=|OM|=√1²+7²=√50=5√2 Albo Punkt przecięcia prostopadłej do k w punkcie M i dwusiecznej kąta MSN jest środkiem szukanego okręgu.