sprawdź ktoś funkcja: Czy w tym przykładzie można wyznaczyć punkt przecięcia z osią x? W odpowiedziach dla tego i jeszcze drugiego przykładu jest podana wynik tylko dla przecięcia z osią y. fx= ^x+3_x²−9 fx=x+3/x²−9

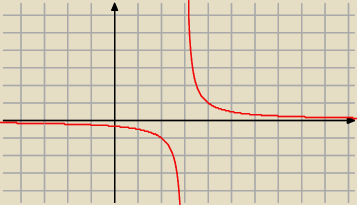
5-latek: To jest nwykres tej funkcji poza tym x²−9=(x+3)(−−3) czyli D_f= R\{−3,3} Miesjce zerowe x+3=0 to x=−3 (sprawdz sobie z dziedzina

funkcja: A jak sprawdzić, patrząc tylko na ten przykład że nie posiada on punktu przecięcia z osią x?

Benny: Jeśli ma przecinać oś x to współrzędna y ma być równa 0

5-latek: 1. Okrslasz dziedzine 2. liczysz miejsce zerowe Sprawdzasz z dziedzina (tak sie postepuje A patrza na ten przyklad to znam wzor skroconego mnozenia a²−b²=(a+b)(a−b) i licze to w pamieci No to zobacz czy np taka funkcja (bez rysowania wykresu ma miejce zerowe

	x−5
y=
	x2−25

y= {x+4}{x²−16}

funkcja: No to podstawiając 0 za y, wychodzi −3.

funkcja: Miejsce zerowe w pierwszym przykładzie wynosi 5, ale dziedzina nie zawiera 5 oraz −5. W drugim przykładzie miejsce zerowe to −4, ale dziedzina nie zawiera 4 oraz −4. Czyli wychodzi na to, że jeśli miejsce zerowe nie występuje w dziedzinie, to go nie ma?

qqaazzxx: Dokładnie tak

funkcja: Teraz już rozumiem. Dzięki za wytłumaczenie.