Proszę o pomoc kochani forumowicze !! :( Głupiutka : Bardzo bym prosiła o pomoc w przebiegu zmienności funkcji x−1/x²+3x−4

daras: sama licz: https://matematykaszkolna.pl/strona/3420.html

Janek191: Tu nie ma funkcji !

	x − 1
f(x) =		?
	x2 + 3 x − 4

qqaazzxx: To tu chyba trzeba policzyć pochodną określić dziedzinę funkcji i pochodnej wyliczyć miejsca zerowe pochodnej i tabelką potem. Pochodna takiej funkcji to m−mianownik l−licznik

	l'×m−l×m'
f'=
	m2

qqaazzxx:

	x−1
Ale to się chyba też da i bez pochodnej bo f(x)=		więc dziedzina to R−{−3,1} i
	(x−1)(x+3)

	1
ta funkcja przyjmuje postać		no i to hiperbola przesunięta o 3 w lewo narysuj sobie i
	x+3

określ przebieg zmienności

Janek191: ( x − 1)*( x + 3) ≠ x² + 3 x − 4

qqaazzxx: Oj pomyłka zamiast x+3 powinno być x+4 więc przesunięcie hiperboli o 4 w lewo a nie 3

5-latek: badanie przebiegu zmiennoci funkcji 1. Wyznaczyc dziedzine funkcji 2. Wyznaczyc punkty przeciecia wykresu z osiami ukladu wspolrzednych 3. Zbadac parzystosc. nieparzystosc i okresowosc funkcji 4. Zbadac granice funkcji na koncach przedzialu(przedzialow wyznaczonych przez dziedzine funkcji 5. Znalezc asymptoty wykresu funkcji 6. Wyznaczyc pierwsza pochodna funkcji w punktach w ktorych ona istnieje 7. Zbadac znak pierwszsej pochodnej aby wyznaczyc przedzialy monotonicznosci 8. Zbadac ekstrema funkcji 9. Wyznaczyc druga pochodna funkcji w punktach w ktorych ona istnieje 10. Zbadac znak drugiej pochodnej aby wyznaczyc przedzialy w ktorych ta funkcja jest wypukla ,wklesla , i aby wyznaczyc punkty przegiecia 11. Sporzadzic tabelke zmiennosci funkcji 12. Narysowac wykres funkcji . Chyba nic nie zapomnialem napisac (duzo czasu minelo Jak widzisz nie jest to praca na 5 minut tylko conajmniej godzine wiec zagladnij do ksiazki i licz

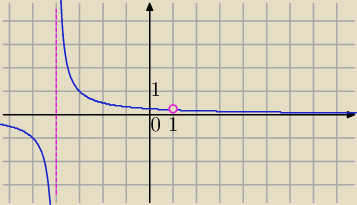
Mila: 1)Przekształcić wzór . ( podał qqaazz...)

	x−1
f(x)=
	(x−1)*(x+4)

2) D: x≠1 i x≠−4

	1
f(x)=		hiperbola , funkcja znana z LO
	x+4

3) Asymptoty : x=−4 pionowa y=0 asymptota pozioma. 4) brak miejsc zerowych 5) funkcja malejąca przedziałami. 6) licz granice