 Czy mógłbym prosić o pomoc w udowodnieniu wzoru na średnią harmoniczną w następujacym linku:
http://tube.geogebra.org/student/m8018
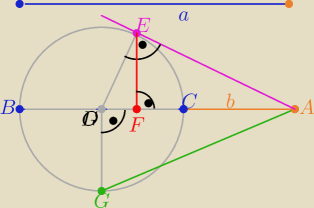
chodzi o zaleznosc |AF| = 2aba+b
Bardzo prosiłbym o oświecenie
Czy mógłbym prosić o pomoc w udowodnieniu wzoru na średnią harmoniczną w następujacym linku:
http://tube.geogebra.org/student/m8018
chodzi o zaleznosc |AF| = 2aba+b
Bardzo prosiłbym o oświecenie 





| a−b | ||
Dla odcinków : |AB|=a , |AC|=b a>b r=|BD|=DE|=DC|= | bo | |
| 2 |
| a−b | ||
|AB|=b+2r ⇒ r= | ||
| 2 |
| a−b | a+b | |||
|AD|=|AC|+r= b+ | = | −−− śr. arytmetyczna | ||
| 2 | 2 |
| a+b | a−b | |||
z tw. Pitagorasa w ΔADE : |AE|2=|AD|2−|DE|2 = ( | )2−( | )2 = ab | ||
| 2 | 2 |
| |AD| | |AE| |
| √ab | ||||||||||
= | ⇒ | = | |||||||||||
| |AE| | |AF| | √ab | |AF| |
| 2ab | ||
to|AF|= | −−− śr. harmoniczna | |
| a+b |
| a−b | a+b | |||
z tw. Pitagorasa w ΔDGA: |AG|2= |DG|2+|AD|2⇒ |AG|2= ( | )2+( | )2 | ||
| 2 | 2 |
| a2+b2 | ||
to |AG|= √ | −−− śr.kwadratowa | |
| 2 |






 ! *KŁANIA SIĘ NISKO*
! *KŁANIA SIĘ NISKO* 

