| a2 | ||
wynik to P = | ||
| 16 |
| b | |
= sin150 ⇒ b = a sin150
| |
| a |
| c | |
= cos150 ⇒ c = a cos150
| |
| a |
| x | AE | AE | |||
= sin150 ⇒ x = EB*sin150 | = cos150 ⇒ y = | ||||
| EB | y | cos150 |
| AE | ||
PDEFG = ( EB*sin150 )*( | )
| |
| cos150 |
| √3 | ||
sin150= (sin450 − 300)= cos300= | ||
| 2 |
| 1 | ||
cos150= (cos450 − 300) = sin300 = | ||
| 2 |
| √3 | √3 | √3 | ||||
to P = (EB* | )(2AE) = | EB*AE = | *AE*(AB − AE)=
| |||
| 2 | 2 | 2 |
| √3 | 1 | |||
= | *AE*( | a − AE)
| ||
| 2 | 2 |
 wynik jest dobry ...
wynik jest dobry ...
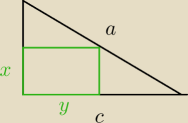
| x | acosx | ||
= tgx c = acosx P = x*y = ctgxy − y2tgx i osiąga maksimum dla: y+ | |||
| c−y | 2 |
| sinxcosx | sinxcosx | |||
Po podstawieniu do wzoru otrzymujemy: P = a2( | − | ) | ||
| 2 | 4 |
| 1 | 1 | a2 | ||||
= a2 ( | − | ) = | ||||
| 8 | 16 | 16 |
| acosx | acosx | asinx | acosx | |||||
P = (acosx − | )*tgx* | = (asinx − | )* | = i licz | ||||
| 2 | 2 | 2 | 2 |
 , ale wynik wychodzi dobry
, ale wynik wychodzi dobry 
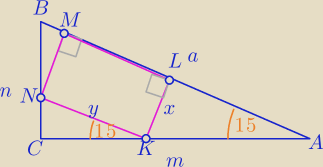 |AC|=m
|BC|=n
|AB|=a
PKLMN=x*y
|AC|=m
|BC|=n
|AB|=a
PKLMN=x*y
| x | ||
tg(15)= | ||
| |AL| |
| |BM| | ||
tg(15o)= | ||
| x |
| cos2(15)+sin2(15) | ||
y=a−x* | ||
| sin(15)*cos(15) |
| 1 | ||||||||
y=a−x* | ||||||||
|
| 1 | ||
a−8x=0 ⇔x= | a | |
| 8 |
| 1 | 1 | a2 | a2 | |||||
P(x)=a* | a−4*( | a)2= | − | ⇔ | ||||
| 8 | 8 | 8 | 16 |
| a2 | ||
P▭= | ||
| 16 |
