Wyznacz współrzędne wierzchołków trapezu Tinlgia: Wszystkie wierzchołki trapezu ABCD, o podstawach AB i CD (|AB|>|CD|), należą do paraboli y=−x²+8x−7, która przecina oś OX w punktach A i B. Wyznacz współrzędne wierzchołków tego trapezu, który ma największe pole i oblicz to pole.

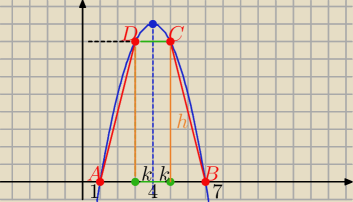
Eta: −x²+8x−7=0 ⇒ (x−1)(x−7)=0 ⇒ x=1 v x= 7 to A(1,0) , B(7,0) i |AB|=6 x_w=4 i treści zad. |AB|>|CD| to punkty C i D leżą nad osią OX i są położone symetrycznie względem prostej x=4 (oś symetrii paraboli) zatem punkty C(4+k, f(4+k)) i D(4−k, f(4−k)) dla k∊(0,3) i |DC|=2k i h(tr)= f(4+k)=f(4−k) ⇒ f(4+k)= ........ = 9−k²

	6+2k
P(tr)=		*(9−k2) ⇒ P(k)=(3+k)2(3−k)
	2

P^'(k)= ........... = −3k²−6k+9 P^'(k)=0 ⇒ k²+2k−3=0 ⇒ k=−3 −− odrzucamy v k=1 dla k=1 pole trapezu jest największe dokończ............ C(.... , ....) , D(..... , ...) P=....

===: P=(3+4−x_D}(−x_D²+8x_D−7) P=−7x_D²+56x_D−49+x_D³−8x_D²+7x_D P=x_D³−15x_D²+63x_D−49 P'=3x_D²−30x_D+63 P'=0 x_D²−10x_D+21=0 √Δ=4 x_D1=3 x_D2=7 z drugiego warunku S_max dla x_D=3 itd

Eta:

Tinlgia: dziękuję ogromnie