pochodne Kinia: Dobry wieczór! Mam problem z tym zadaniem i bardzo proszę o pomoc , bo nie wiem jak mam przeprowadzić ten dowód Uzasadnij, że prosta o równaniu y=2x+7 jest styczna do wykresu funkcji f określonej wzorem: f(x)=x³−10x−9.

azeta: najprościej: jak znaleźć kandydata na punkt styczności ? rozwiązać równanie x³−10x−9=2x+7, mając już punkt (albo dwa) będzie łatwo wykazać że podana prosta jest styczna do tego wykresu właśnie w którymś z tych punktów

AS: Szukam punktu wspólnego krzywej i prostej x³ − 10*x − 9 = 2*x + 7 czyli x³ − 12*x − 16 = 0 Wyróżnik tego równania D = q²/4 + p³/27 D = (−16)²/4 + (−12)³/27 = 0 a to świadczy o jedynym rozwiązaniem.

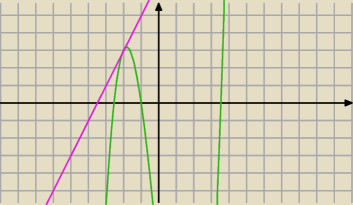
ax: f'(x)=3x²−10 podstawiając 3x²−10=2 ⇒ x²=4 ⇒ x_s=−2 y_s=3 x=2 odpada ....bo ?

Janek191: 2 x + 7 = x³ − 10 x − 9 x³ − 12 x − 16 = 0 x = 4 64 − 48 − 16 = 0 ( x³ − 12 x − 16) : ( x − 4) = x² + 4 x + 4 − x³ + 4 x² −−−−−−−−−− 4 x² − 12 x − 4 x² + 16 x −−−−−−−−−−− 4 x − 16 − 4 x + 16 −−−−−−−−−− 0 oraz ( x + 2)² = 0 x = − 2 y = 2*(−2) + 7 = 3 P = ( − 2, 3) punkt styczności y' = f '( x) = 3 x² − 10 y'( − 2) = 3*( −2)² − 10 = 12 − 10 = 2 = a współczynnik kierunkowy danej prostej.