Nierówność z modułem, rozwiąż nierówność Reqe: Rozwiąż nierówność |x|−|x−4|≤6−x Może mi ktoś krok po kroku wytłumaczyć jak się takie zadania rozwiązuje? Proszę

Metis: Rozwiązujesz przedziałami https://matematykaszkolna.pl/strona/1806.html

Metis: https://matematykaszkolna.pl/strona/1805.html

Reqe: Dziękuje, jak będę miał jakieś pytanka to napisze

Metis: Pisz, pytaj

Reqe: Ok, więc rozwiązałem zadanie prawidłowo, jednak mam pytanie odnośnie pierwszego przedziału, mianowicie (−∞;0) Zgodnie z informacjami zawartymi na stronie, którą podlinkowałeś rozumiem, że mam rozpisać |x| jako x≥0 (bo rozpisuje pierwszy moduł). Robię to tak samo jak na tej stronie: https://matematykaszkolna.pl/strona/1806.html i o ile u nich 1 moduł wynosi x+3 i on ma być większy od 0 to x+3≥0 x≥−3 x∊<−3;∞) To u mnie jest sam X x≥0 więc x ∊<0;∞) Jednakże przedział ten ma być (−∞;0) a nie (0;∞). Nie do końca rozumiem P.S. Jak coś to wiem kiedy pisać "< ; >" a kiedy "( ; )"

Metis: Zapisz całe rozwiązanie.

Reqe: Tzn rozwiązanie mam poprawne, tylko jak mi wychodzą przedziały: (−∞;0),<0;4>,(4,∞+) to nie do końca rozumiem skąd ten pierwszy przedział mi wyszedl. Dlaczego (−∞;0) a nie (0;∞) Wynik mi wyszedł <−2;2>

Metis: Rozwiązanie to pikuś. Pokaż jak rozwiązujesz...

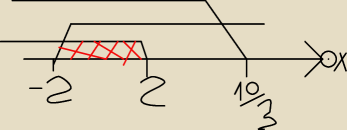
Reqe: dla x ∊ (−∞;0) −x−x+4≤6−x x≥−2 x∊<−2;0) dla x∊ <0;4> x−x+4≤6−x x≤2 x∊<0;2> dla x ∊ (4;∞+) x+x−4≤6−x 3x≤10 x≤10/3 poźniej rysuje oś OX i zaznaczam te punkty (−2;2;10/3) i od nich wyprowadzam "linie" w zależności od przedziału i biorę część wspolną jako odp <−2.2> Sorki za prymitywny rysunek, jednak jak probowałem normalnie liczby napisać to co chwila mi się czyściło

daras: a skąd masz przedział <0;2>

	10
rozw: x ≤
	3

Metis: Proponuję taki zapis : |x|−|x−4|≤6−x Rozwiązuje w przedziałach: 1) x∊(−∞,0) 2) x∊[0,4) 3) [4,+∞) 1) Dla x∊(−∞,0) nierówność przyjmuje postać: −x−[−(x−4)]≤6−x −x−[−x+4]≤6−x −x+x−4≤6−x −x+x+x≤6+4 x≤10 x∊(−∞,10] Zatem x∊(−∞,0) 2) Dla x∊[0,4) nierówność przyjmuje postać: x−[−(x−4)]≤6−x x[−x+4]≤6−x x+x−4≤6−x x+x+x≤6+4 3x≤10

	10
x≤
	3

	10
x∊(−∞,		]
	3

	10
Zatem x∊[0,		]
	3

3) Dla [4,+∞) nierówność przyjmuje postać: x−(x−4)≤6−x x−x+4≤6−x x−x+x≤6−4 x≤2 x∊(−∞,2] Brak rozwiązania. Sumujemy uzyskane odpowiedzi:

	10
x∊(−∞,0) U [0,		] , stąd
	3

	10
x∊(−∞,		]
	3

=========================================

Reqe: przedział <0;> stąd, iż te "x" miały być mniejsze /równe od 2 dla x w przedziale <0;4> a mi wyszedł x≤<2 a nie może być mniejszy od 0 więc przy 0 domykam.

Metis: Jak widzisz, wynik masz dobry , a rozwiązanie

Reqe: Ja to robię wraz z rozwiązaniami z matury, tam też jest napisane <−2, 2> jako odp. Również gdy wpisze się przykład |x|−|x−4|≤6−x w google − to pierwszy wynik wyszukiwania wyjdzie http://www.zadania.info/d563/5219321 gdzie również odp. krok po kroku wynosi <−2.2>. Trochę już jestem zdezorientowany

Metis: A nie, jednak wynik też masz zły

Metis: |x|−|x−4|≤6−x≠ |x|+|x−4|≤6−x

Reqe: O Boże, przepraszam za kłopot. Ja cały czas liczyłem dla + chociaż napisałem na początku − Jednak i tak na szczęscie rozumiem już jak się rozwiązuje takie przykłady Czyli w sumie o to chodziło, tylko niestety zająłem Twój czas przez moj bład, za co przepraszam :c

daras: reqe korzystasz z błednych rozwiązań na swoja odpowiedzialność

daras: szkoda czasu na takich... idę na

Reqe: @daras tzn odpowiedzi są prawidłowe, tylko ja niestety Tutaj zapisałem źle podpunkt

Metis: Twoje zdrowie